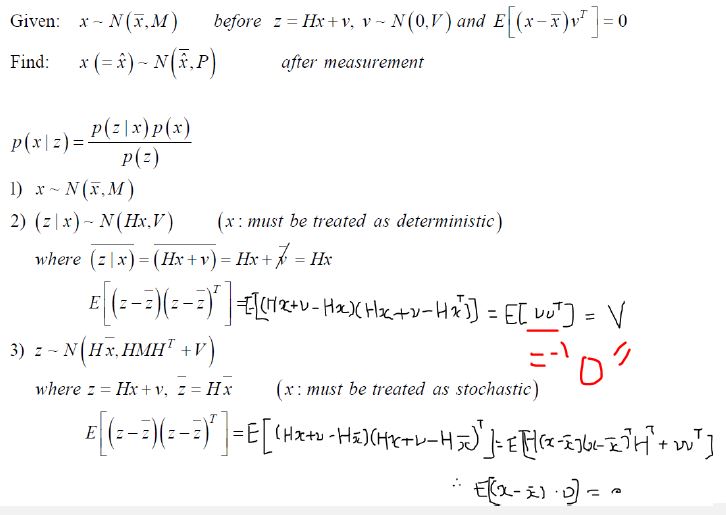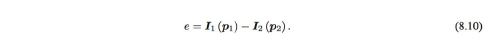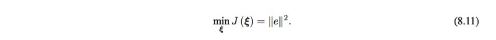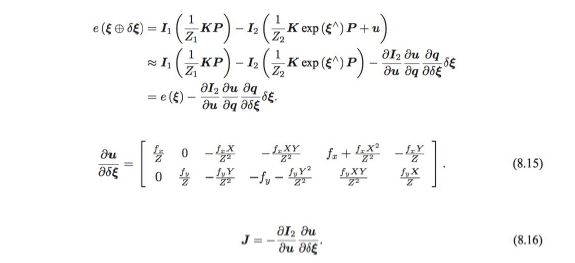18. Pose estimation[Backend] (Bundle Adjustment)
21 Jun 2020 | Visual SLAM
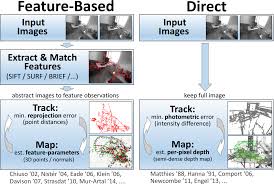
Recap(Feature based Visual Odometer)
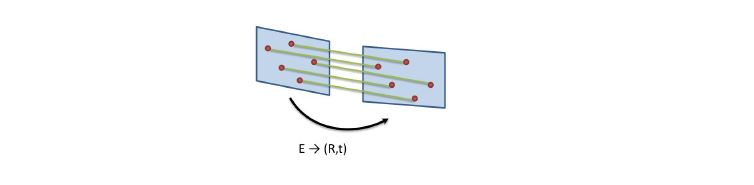
- Relative Camera Pose From 2 views:
- Fundamental Matrix
- Essential Matrix(Fundamental matrix와 Camera 내부 파라미터를 연결하여 구하는 카메라 포즈)
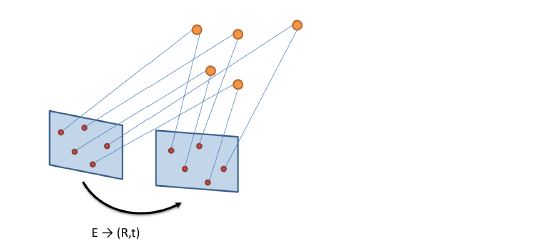
- 3D points
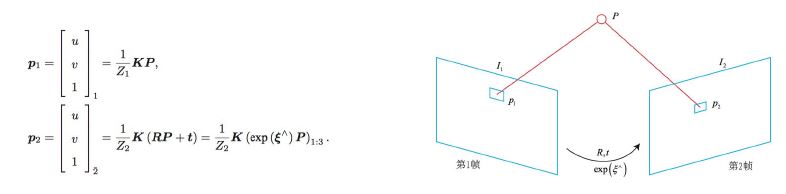
- Triangulation(3D 공간에 있는 X Pose의 값(X,Y,Z)를 가지고 타임스태프 프레임에 비쳐줘는 X Pose값과 이전 프레임에 비쳐진 X Pose값을 가지고 카메라 포즈 구하는 것)
- Subsequent views:
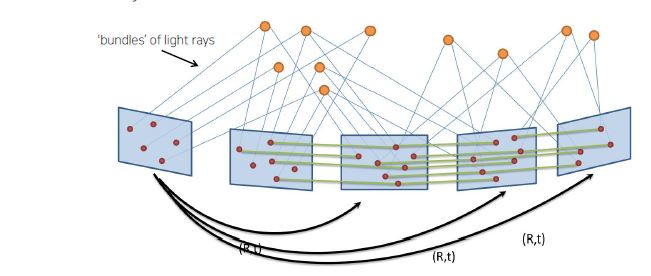
- Bundle Adjustment - 모든 카메라 포즈와 3차원 점을 조정(최적화)한다.
- 각 프레임에 비춰지는 공통된 Feature Point(3D Mappoints)를 최적화 하여(Batch 방법) MapPoints의 pose와 Camera Pose를 동시에 업데이트 한다.
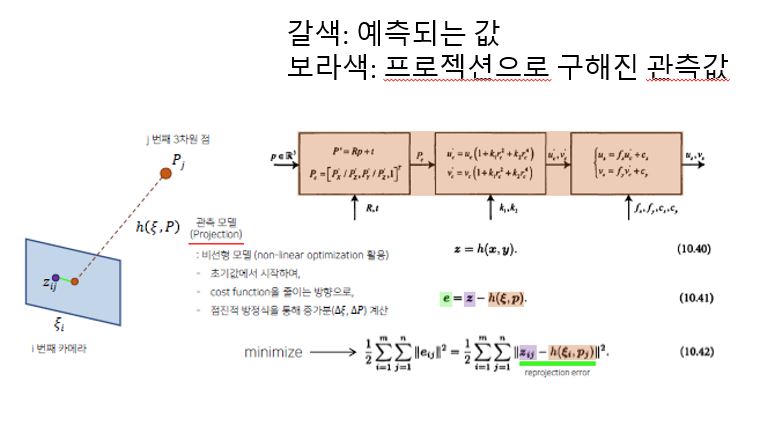
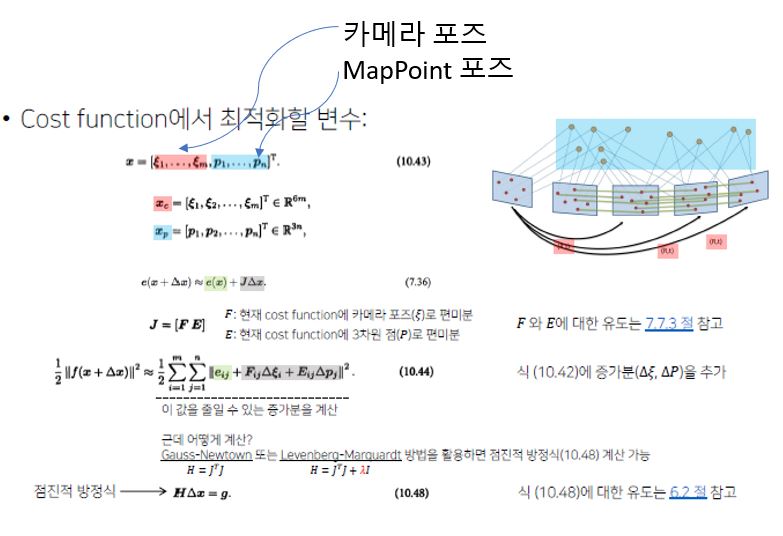
Bundle Adjustment Cost Function
- 최적화하고자 하는 BA Const FUnstions은
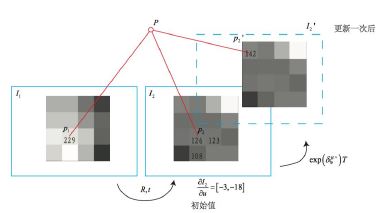
- Total Reprojection error를 줄이는 방법으로 최적화
- Batch 방법으로 Error Reduction 한다. 왜? 적은 값으로는 정확하지 않기 때문에(Noise, Feature 문제)
- Bundle Adjustment 방법은 매 프레임마다 적용할 수 없다
- H 매트릭스 사이즈가 커지기 때문이다.
- 그렇기 때문에 KeyFrame(조건: Feature point 등의 쓰레시홀드에 만족하는 조건) 을 뽑아 BA를 수행한다.
- Keyframe에는 보통 Camera Pose 정보와 MapPoints들의 정보 Covisibility(KeyFrame간 중복되는 Mappoint)등이 저장 되어 있다.
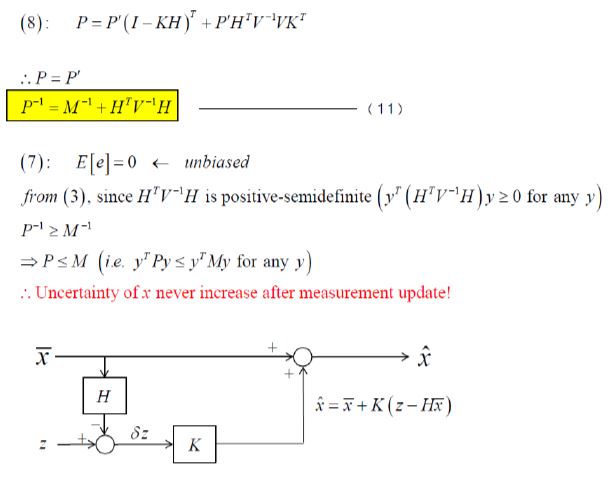
- MapPoints의 x,y,z를 Reprojection하여 error를 최소하하였을때 Camera pose에 대한 오류가 생길 수 있다.
- 그렇기 떄문에 에러를 최소화할때 MapPoint의 위치를 보정하는 것 뿐만아니라 동시에 Camera Pose도 보정 한다.
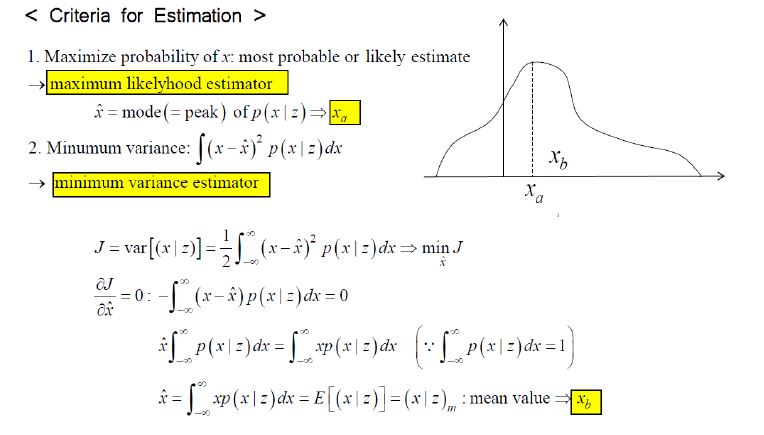
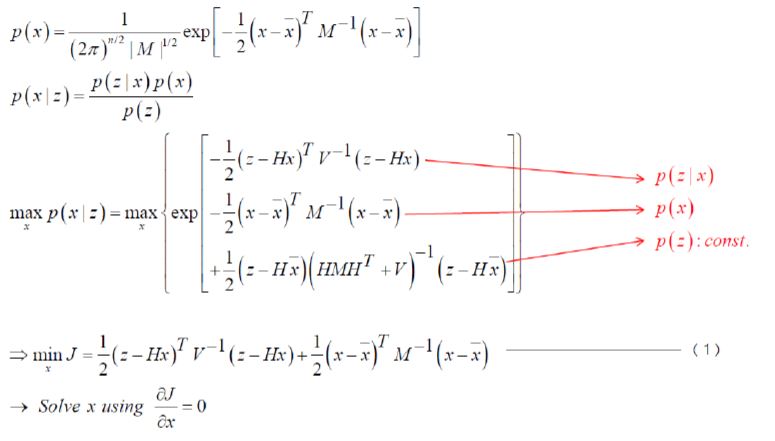
- BA는 기본적으로 Least Square 기반이다.
- 보정은 Incremental 방식인 Kalman Filter보다 Batch 방식의 BA가 더 효과적이다. 그렇기 떄문에 Backend에서는 BA방식이 좋다
-
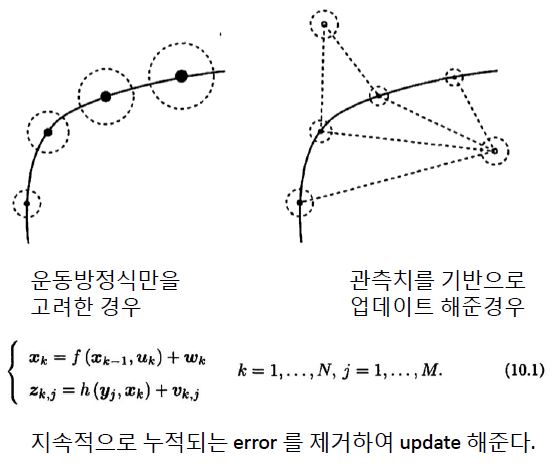
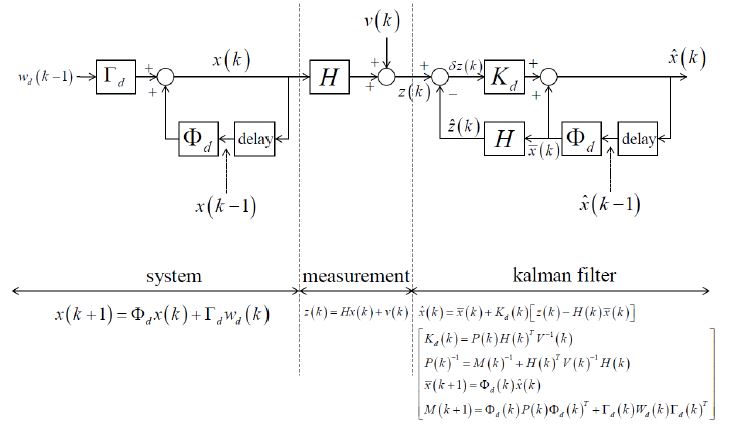
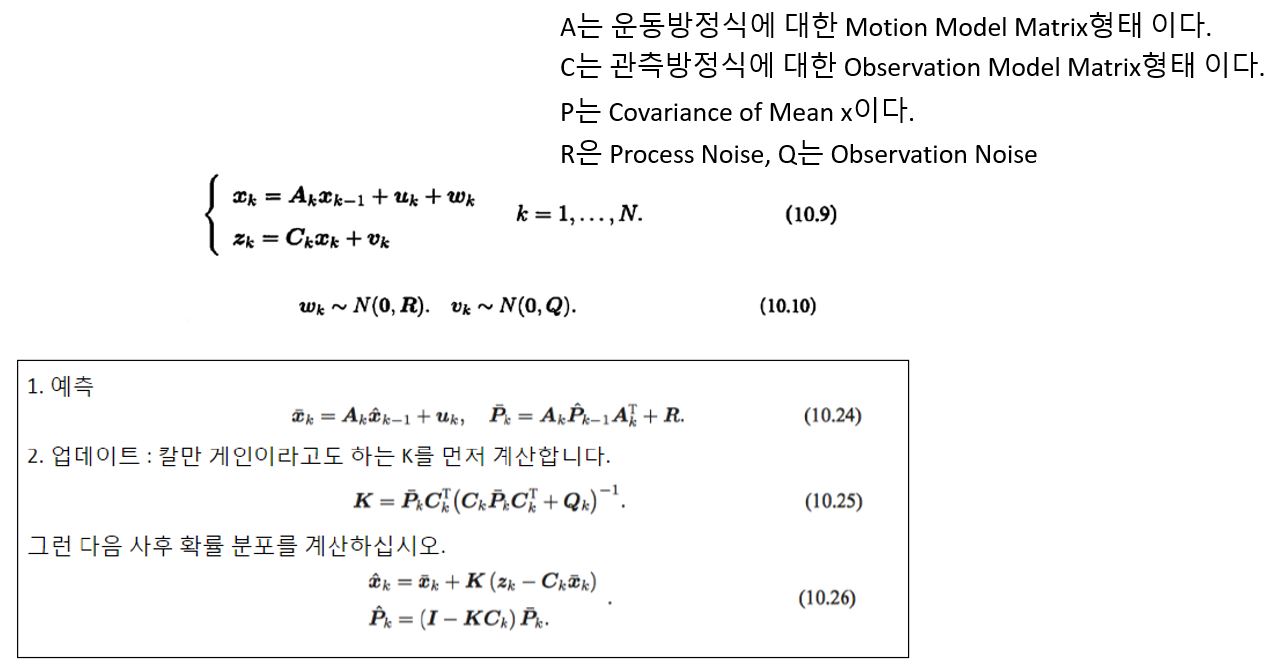
그러므로 두 방법 모두 역할이 나누어져 있는데 Pose Estimation을 할떄 주로 Backend(여러 프레임으로 부터 얻어진 Mappoints와 Camera Pose 데이터 보정) 부분은 BA, Localization 부분은 Kalman Filter(Visual odometer(관측방정식(보통 BA 보정으로 얻어지는 값))과 wheel odometer(운동방정식))을 사용한다.
- 즉 전체적인 시스템은 BA, 순간적인 데이터(프레임이 빠른) EKF.
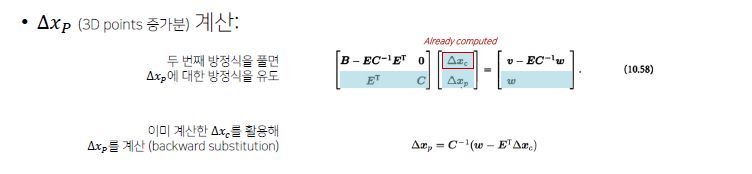
증가분(Incremental Δ) 계산을 위한 점진적 방식은
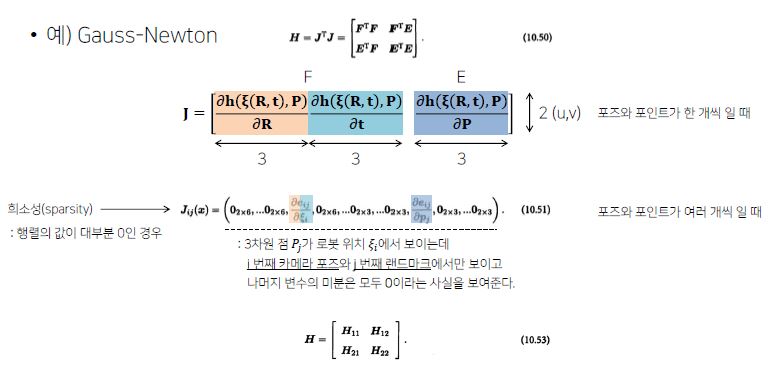
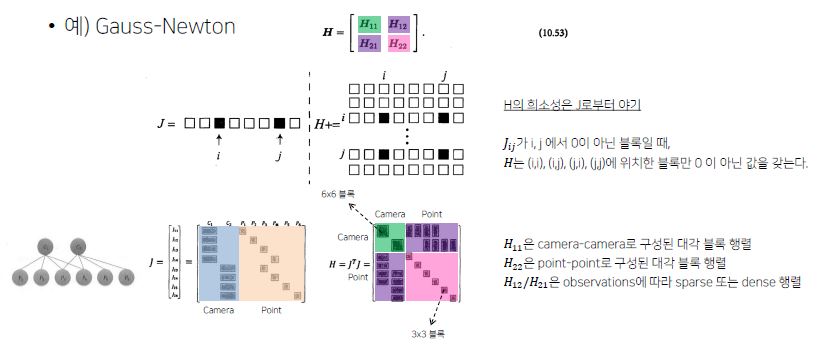
H (Hessian Matrix)
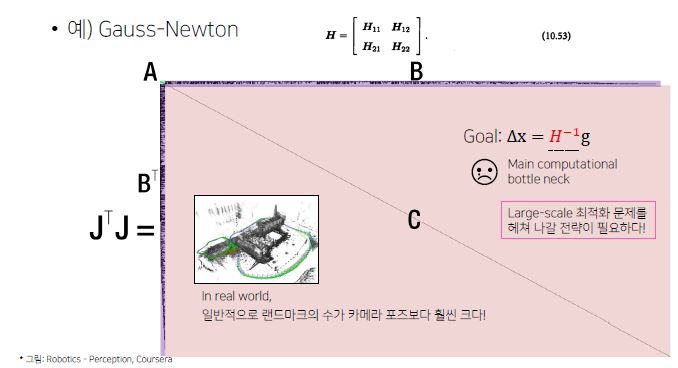
- 예를 들어 100개 프레임에서 관측된 MapPoints의 수가 만개라고 하였을떄
- A는 100 x 100이며, C는 10000 x 10000 크기가 된다.
- 즉 large scale에서 연산량이 어마 무시해진다.
- 연산량을 즐이는 방법을 알아봐야한다.
- A의 구조가 더 작기 떄문에 delta x_c를 먼저 계산한다.
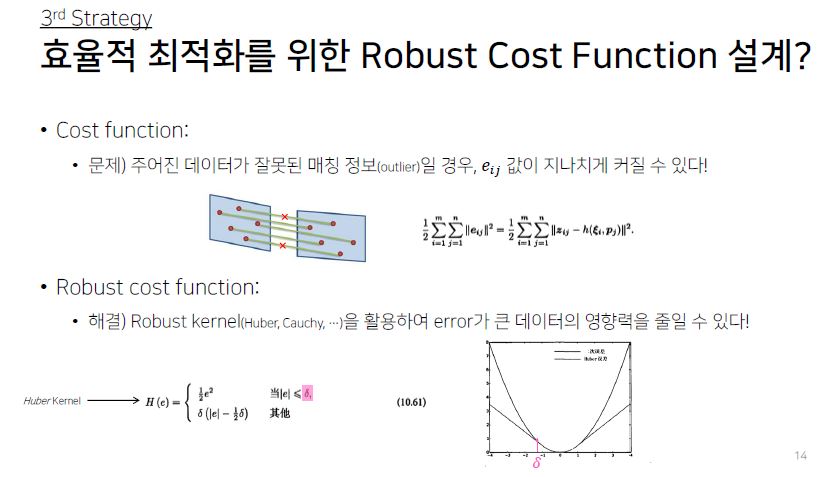
- Robust Cost Function(Error 값이 커지는 것을 방지)은 종류가 많다.
Reference
SLAM KR
Recap(Feature based Visual Odometer)
- Relative Camera Pose From 2 views:
- Fundamental Matrix
- Essential Matrix(Fundamental matrix와 Camera 내부 파라미터를 연결하여 구하는 카메라 포즈)
- 3D points
- Triangulation(3D 공간에 있는 X Pose의 값(X,Y,Z)를 가지고 타임스태프 프레임에 비쳐줘는 X Pose값과 이전 프레임에 비쳐진 X Pose값을 가지고 카메라 포즈 구하는 것)
- Subsequent views:
- Bundle Adjustment - 모든 카메라 포즈와 3차원 점을 조정(최적화)한다.
- 각 프레임에 비춰지는 공통된 Feature Point(3D Mappoints)를 최적화 하여(Batch 방법) MapPoints의 pose와 Camera Pose를 동시에 업데이트 한다.
- Bundle Adjustment - 모든 카메라 포즈와 3차원 점을 조정(최적화)한다.
Bundle Adjustment Cost Function
- 최적화하고자 하는 BA Const FUnstions은
- Total Reprojection error를 줄이는 방법으로 최적화
- Batch 방법으로 Error Reduction 한다. 왜? 적은 값으로는 정확하지 않기 때문에(Noise, Feature 문제)
- Bundle Adjustment 방법은 매 프레임마다 적용할 수 없다
- H 매트릭스 사이즈가 커지기 때문이다.
- 그렇기 때문에 KeyFrame(조건: Feature point 등의 쓰레시홀드에 만족하는 조건) 을 뽑아 BA를 수행한다.
- Keyframe에는 보통 Camera Pose 정보와 MapPoints들의 정보 Covisibility(KeyFrame간 중복되는 Mappoint)등이 저장 되어 있다.
- MapPoints의 x,y,z를 Reprojection하여 error를 최소하하였을때 Camera pose에 대한 오류가 생길 수 있다.
- 그렇기 떄문에 에러를 최소화할때 MapPoint의 위치를 보정하는 것 뿐만아니라 동시에 Camera Pose도 보정 한다.
- BA는 기본적으로 Least Square 기반이다.
- 보정은 Incremental 방식인 Kalman Filter보다 Batch 방식의 BA가 더 효과적이다. 그렇기 떄문에 Backend에서는 BA방식이 좋다
-
그러므로 두 방법 모두 역할이 나누어져 있는데 Pose Estimation을 할떄 주로 Backend(여러 프레임으로 부터 얻어진 Mappoints와 Camera Pose 데이터 보정) 부분은 BA, Localization 부분은 Kalman Filter(Visual odometer(관측방정식(보통 BA 보정으로 얻어지는 값))과 wheel odometer(운동방정식))을 사용한다.
- 즉 전체적인 시스템은 BA, 순간적인 데이터(프레임이 빠른) EKF.
증가분(Incremental Δ) 계산을 위한 점진적 방식은
H (Hessian Matrix)
- 예를 들어 100개 프레임에서 관측된 MapPoints의 수가 만개라고 하였을떄
- A는 100 x 100이며, C는 10000 x 10000 크기가 된다.
- 즉 large scale에서 연산량이 어마 무시해진다.
- 연산량을 즐이는 방법을 알아봐야한다.
- A의 구조가 더 작기 떄문에 delta x_c를 먼저 계산한다.
- Robust Cost Function(Error 값이 커지는 것을 방지)은 종류가 많다.
Reference
SLAM KR