for Robot Artificial Inteligence

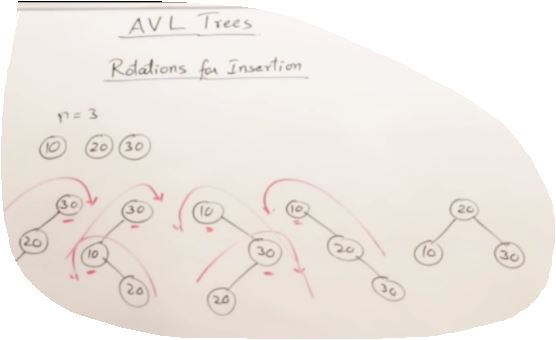
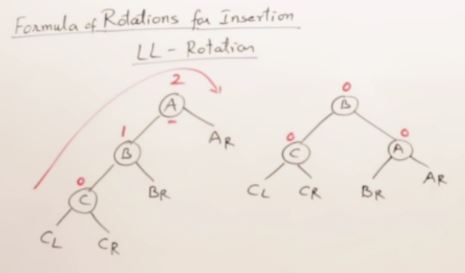
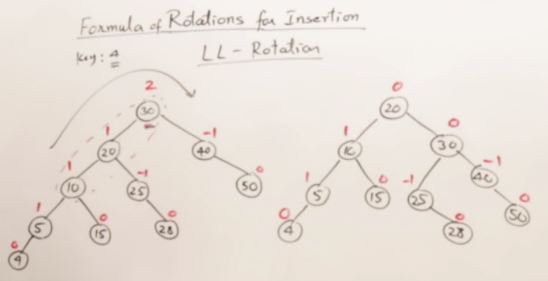
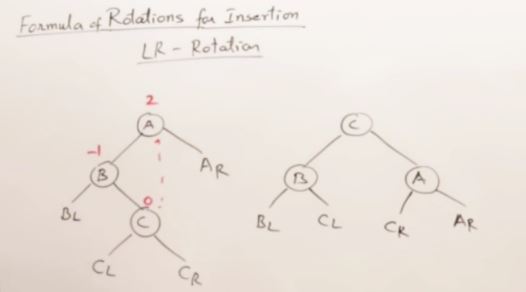
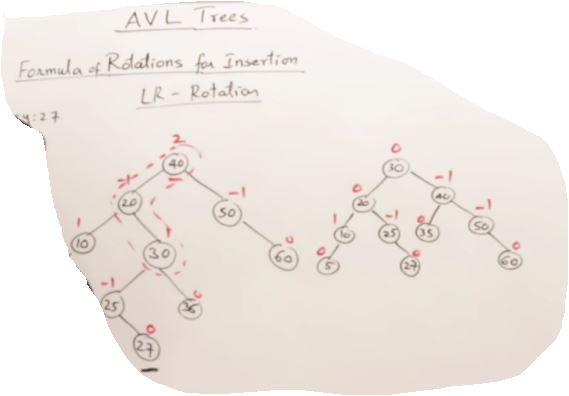
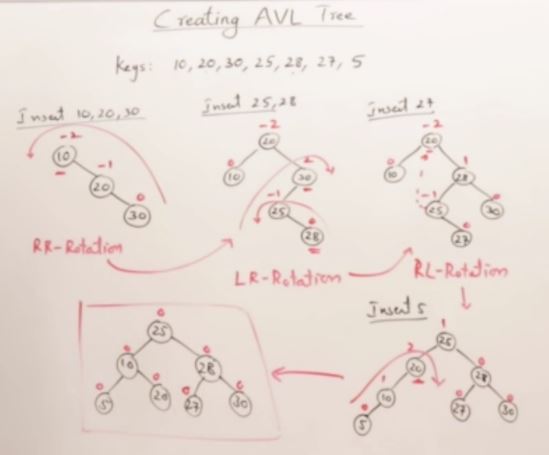
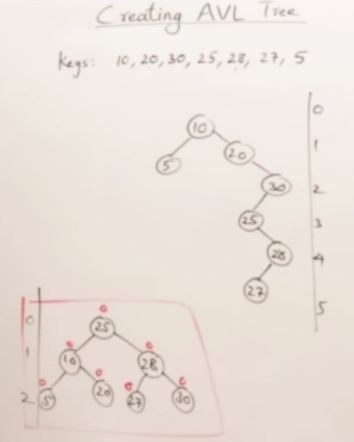
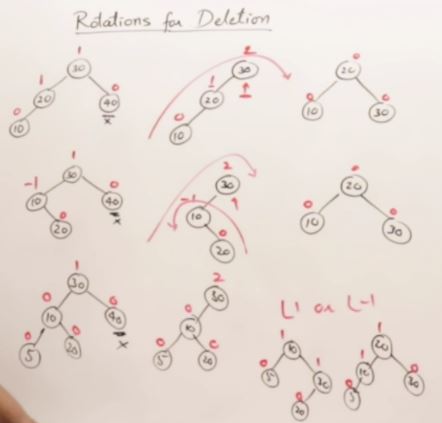
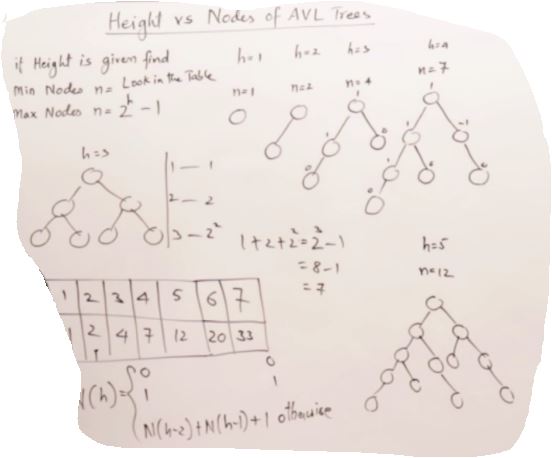
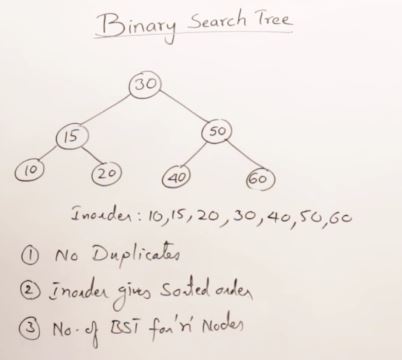
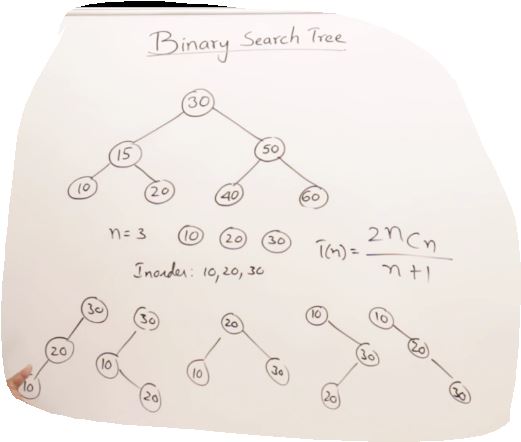
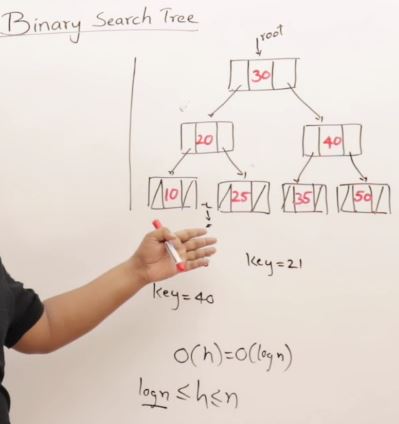
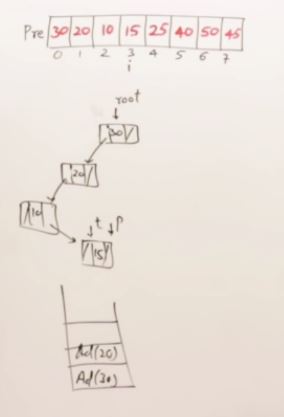
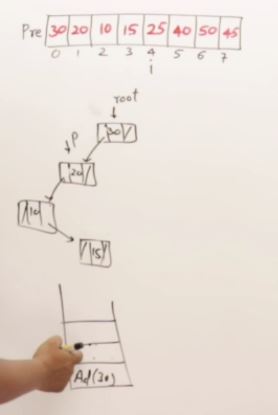
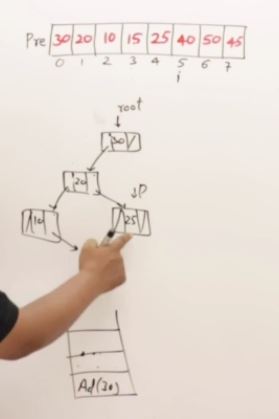
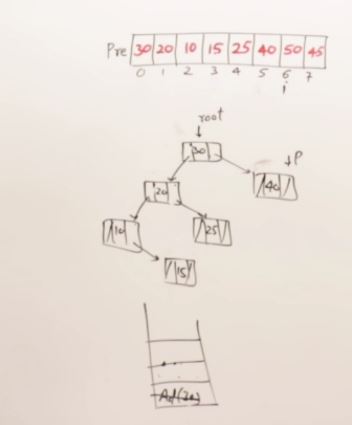
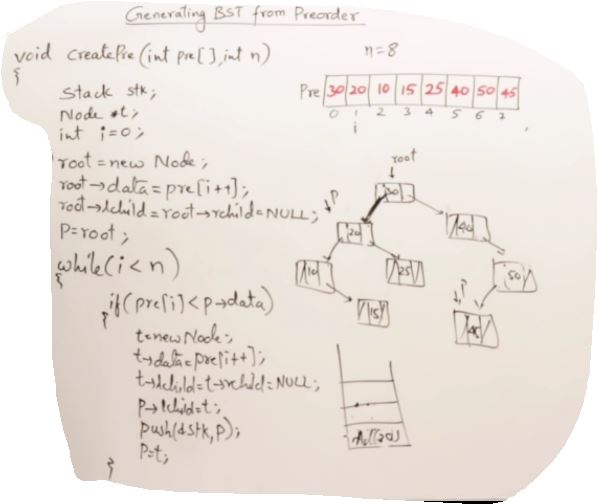
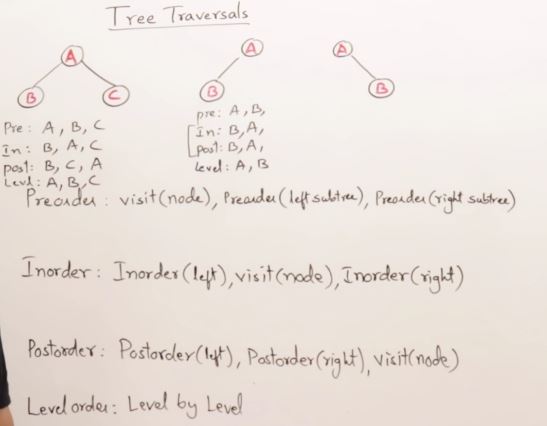
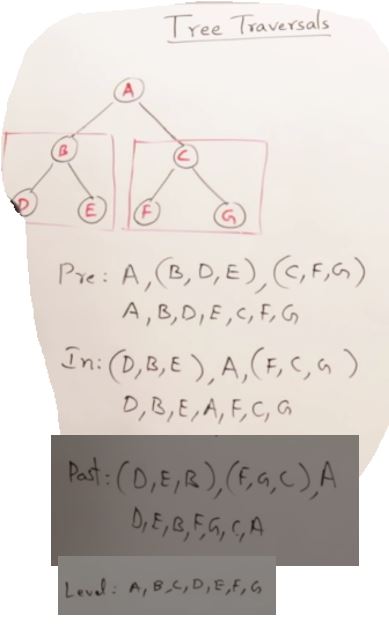
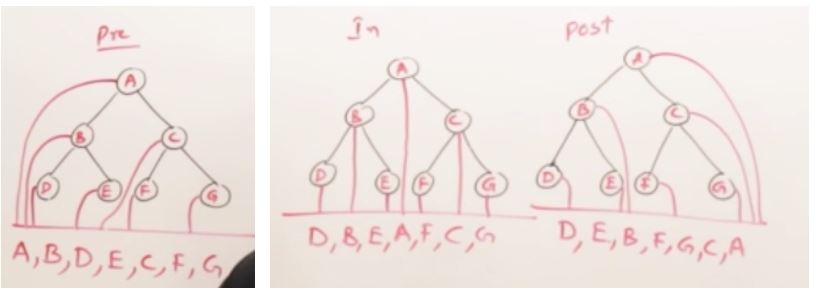
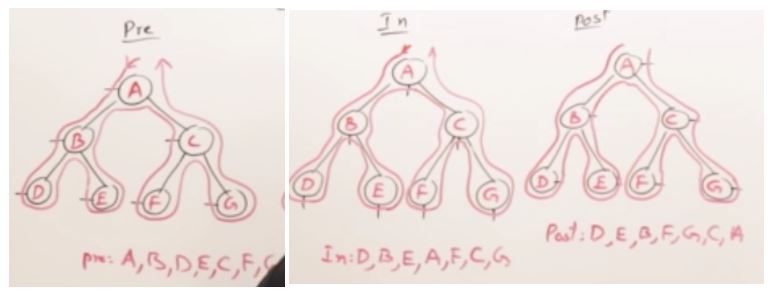
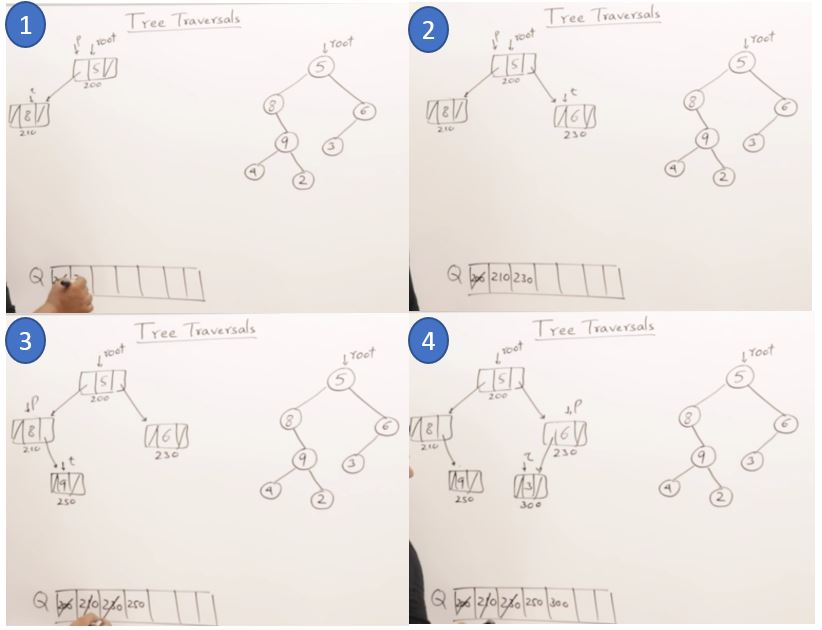
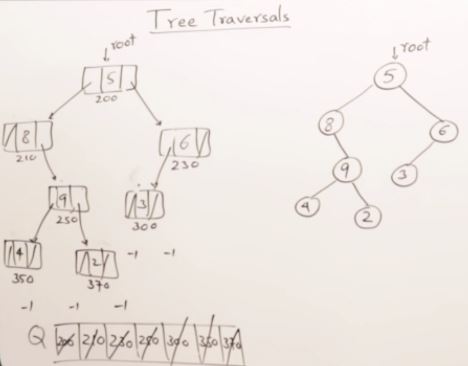
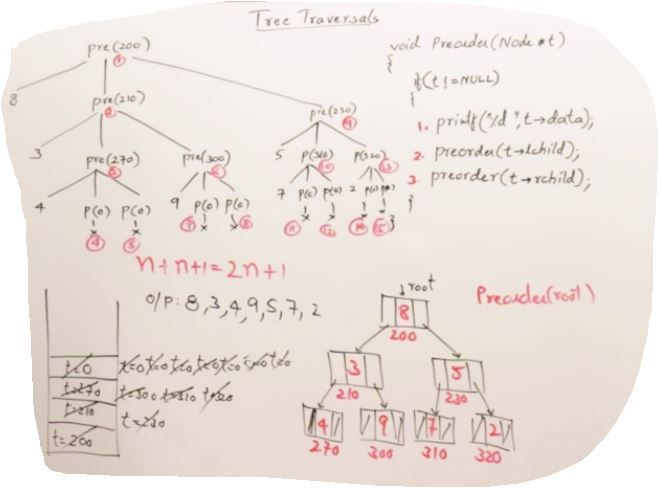
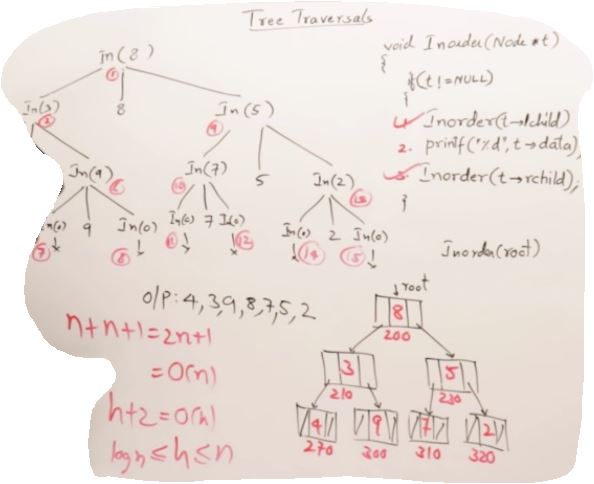
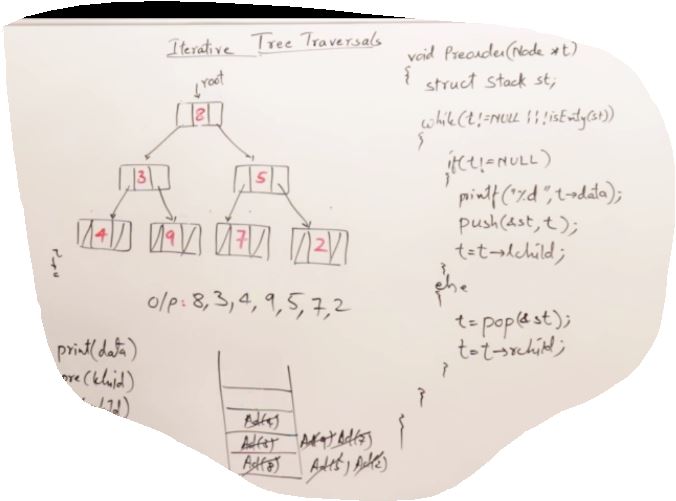
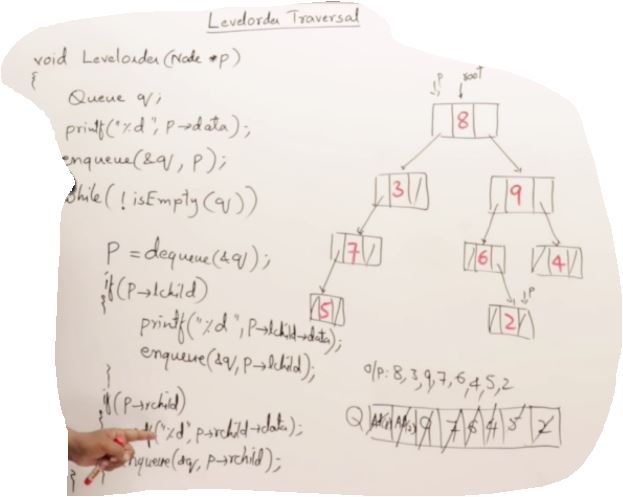
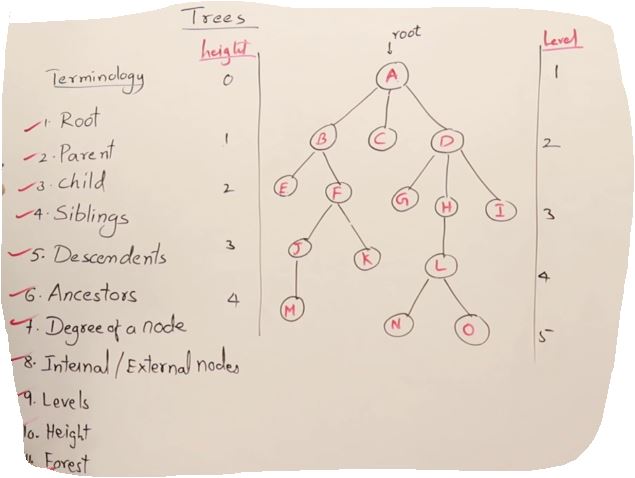
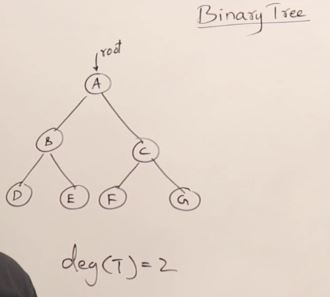
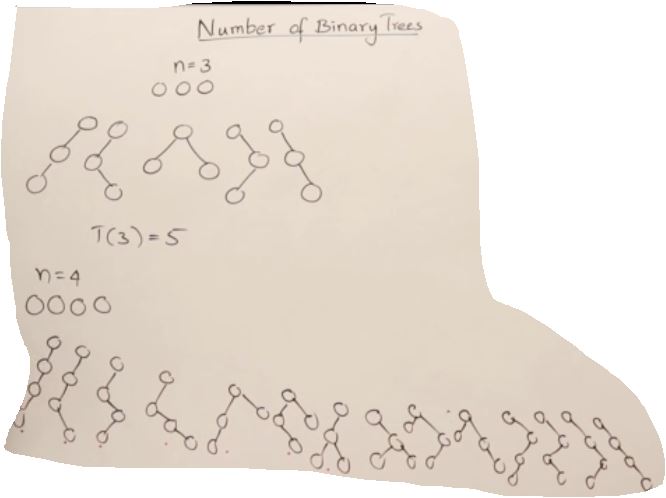
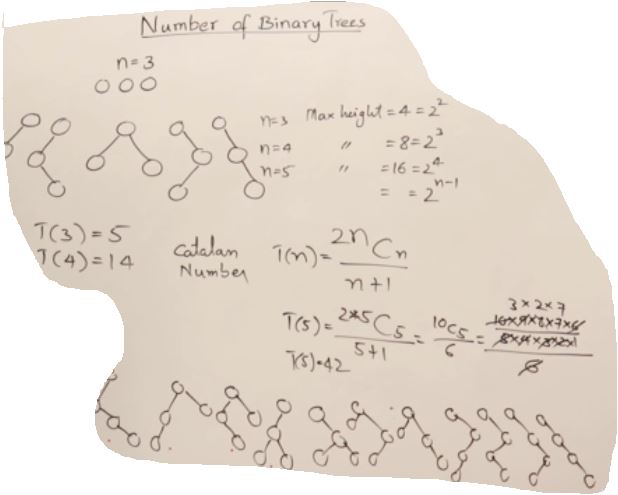
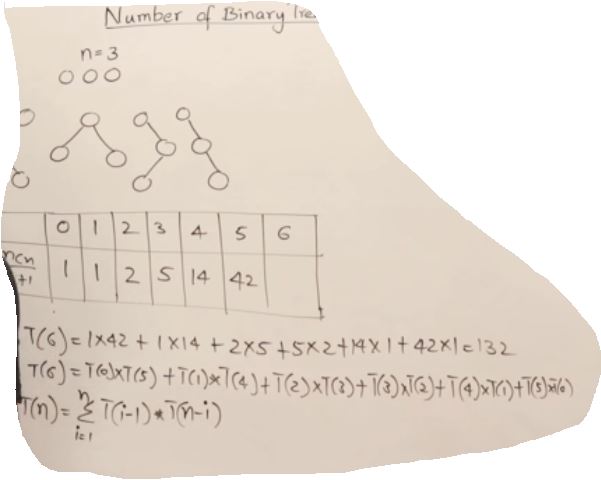
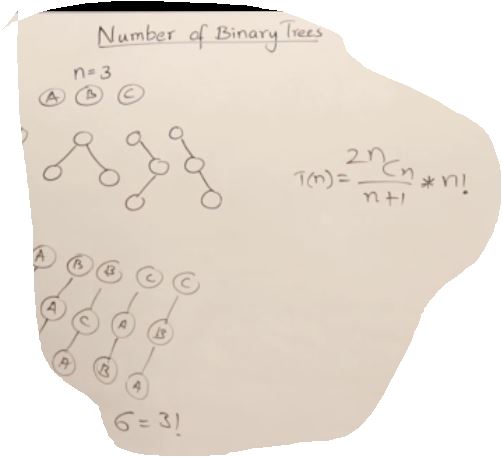
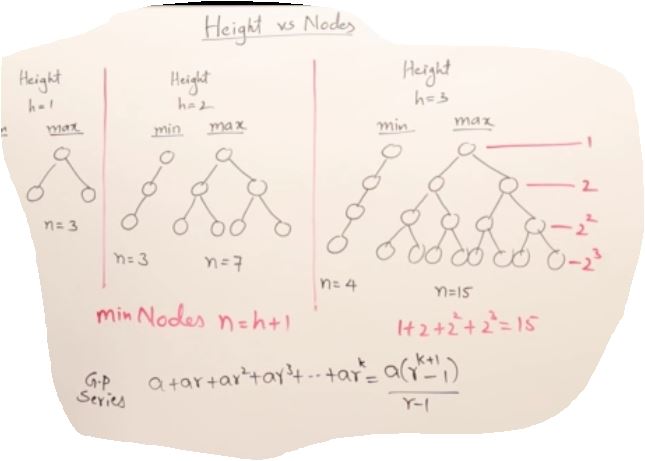
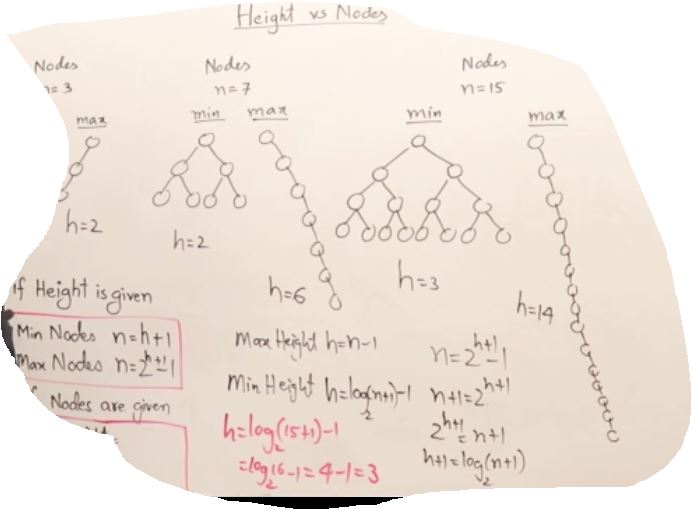
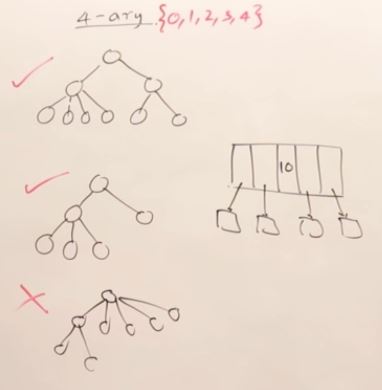
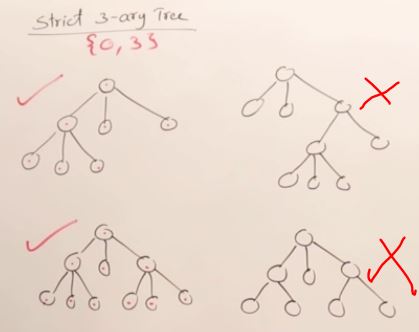
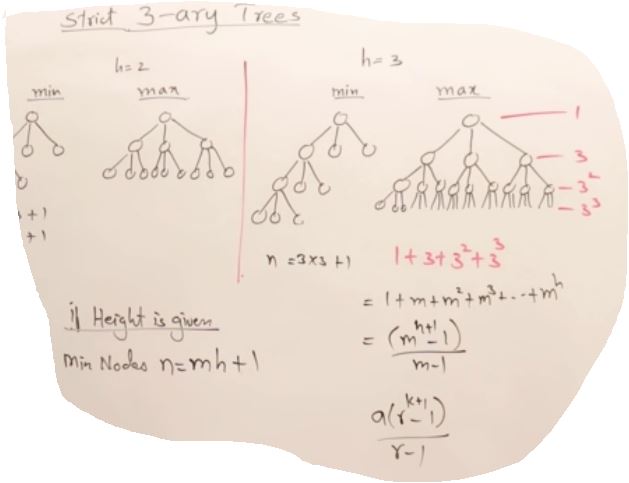
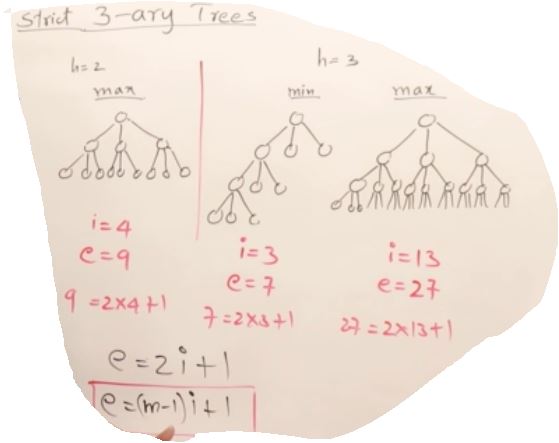
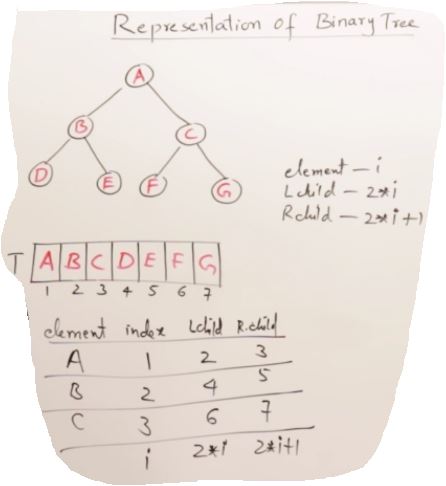
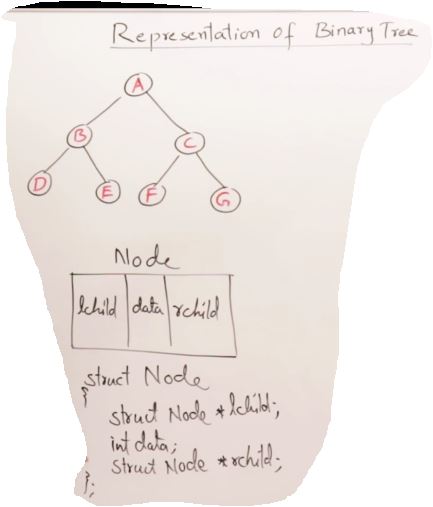
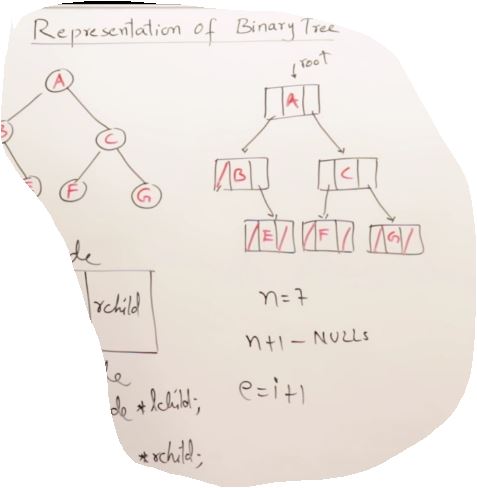
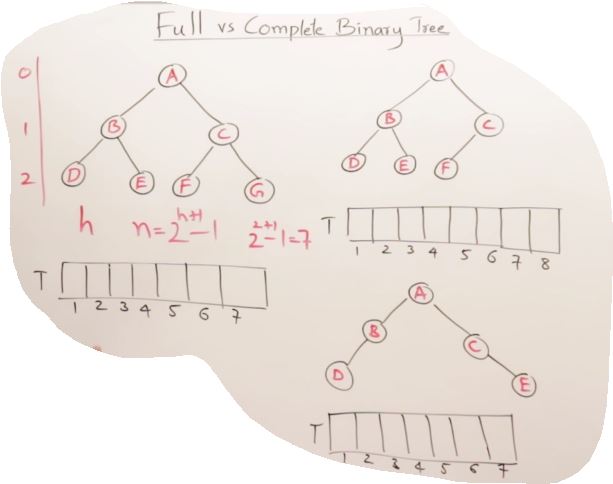
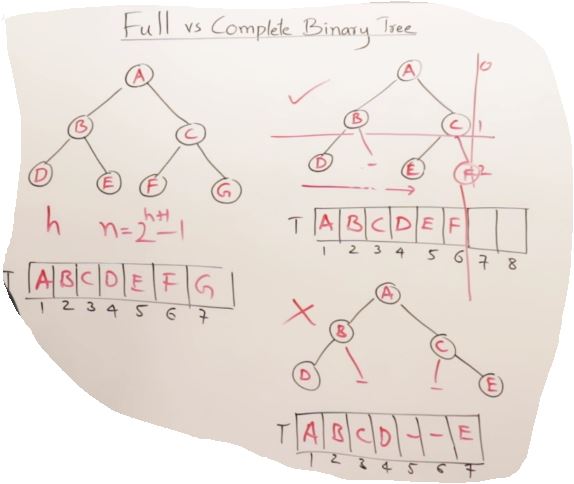
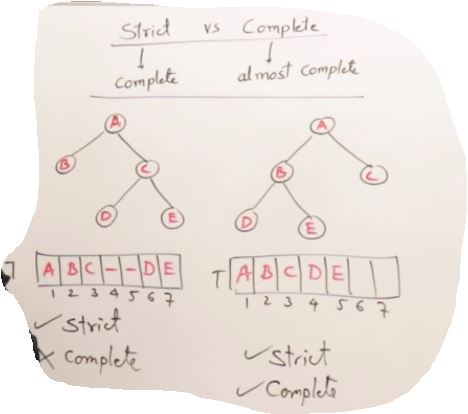
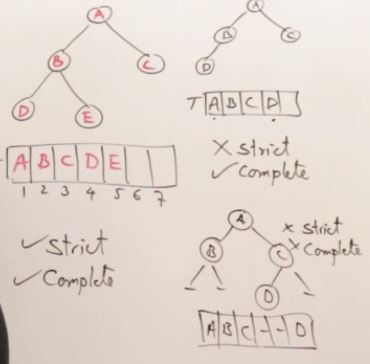
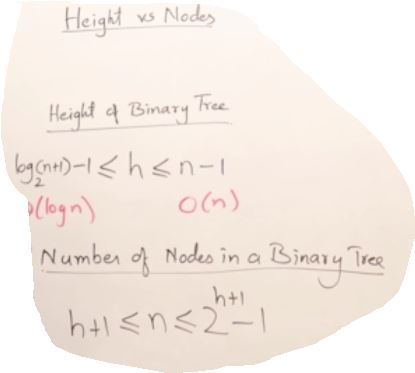27. AVL Trees(Self-balancing binary search tree)

19 Jun 2020 | Algorithm

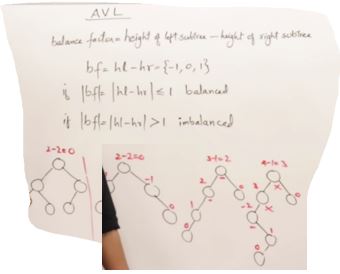
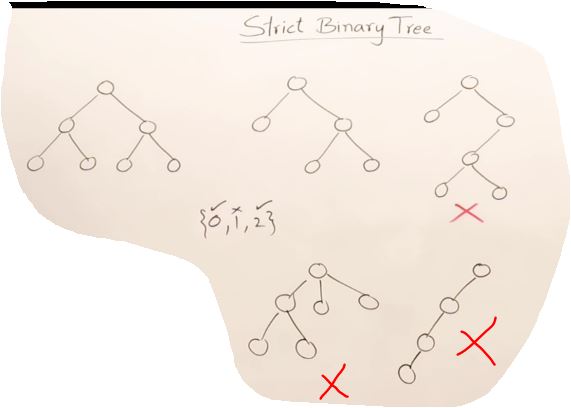
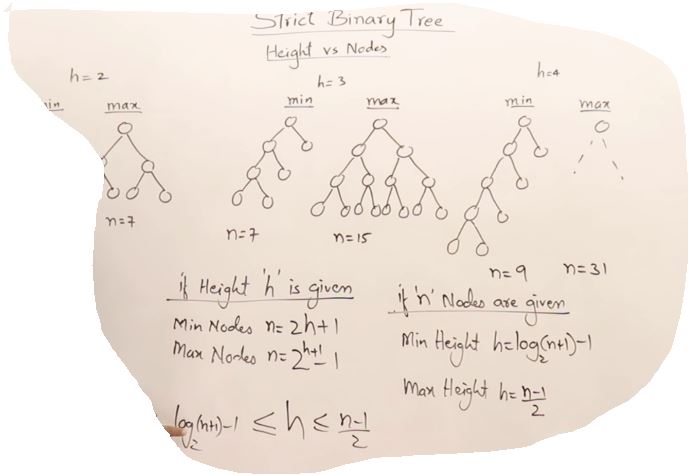
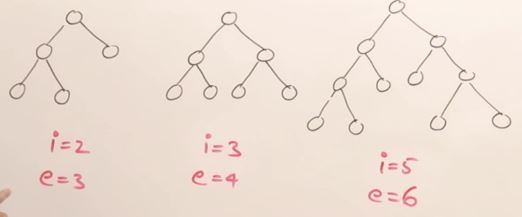
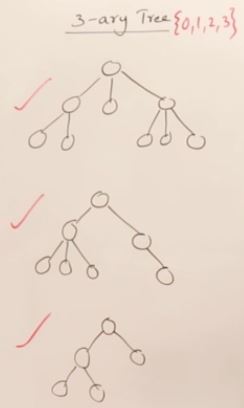
Drawback Binary Search Tree

Introduction to AVL Trees

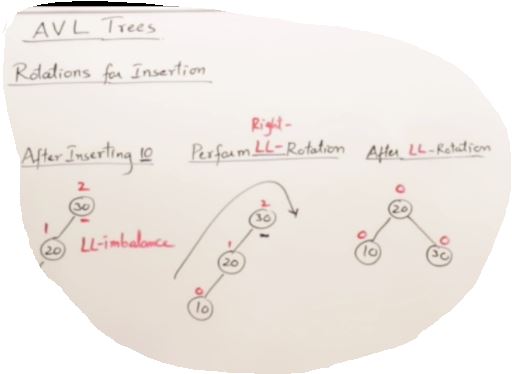
LL and RR Rotation on AVL

#include <iostream>

using namespace std;

class Node {
public:
    Node* lchild;
    int data;
    Node* rchild;
    int height;
};

class AVL{
public:
    Node* root;

    AVL(){ root = nullptr; }

    // Helper methods for inserting
    int NodeHeight(Node* p);
    int BalanceFactor(Node* p);
    Node* LLRotation(Node* p);
    Node* RRRotation(Node* p);
    Node* LRRotation(Node* p);
    Node* RLRotation(Node* p);

    // Insert
    Node* rInsert(Node* p, int key);

    // Traversal
    void Inorder(Node* p);
    void Inorder(){ Inorder(root); }
    Node* getRoot(){ return root; }
};

int AVL::NodeHeight(Node *p) {
    int hl;
    int hr;

    hl = (p && p->lchild) ? p->lchild->height : 0;
    hr = (p && p->rchild) ? p->rchild->height : 0;

    return hl > hr ? hl + 1 : hr + 1;
}

int AVL::BalanceFactor(Node *p) {
    int hl;
    int hr;

    hl = (p && p->lchild) ? p->lchild->height : 0;
    hr = (p && p->rchild) ? p->rchild->height : 0;

    return hl - hr;
}

Node* AVL::LLRotation(Node *p) {
    Node* pl = p->lchild;
    Node* plr = pl->rchild;

    pl->rchild = p;
    p->lchild = plr;

    // Update height
    p->height = NodeHeight(p);
    pl->height = NodeHeight(pl);

    // Update root
    if (root == p){
        root = pl;
    }
    return pl;
}

Node* AVL::RRRotation(Node *p) {
    Node* pr = p->rchild;
    Node* prl = pr->lchild;

    pr->lchild = p;
    p->rchild = prl;

    // Update height
    p->height = NodeHeight(p);
    pr->height = NodeHeight(pr);

    // Update root
    if (root == p){
        root = pr;
    }
    return pr;
}

Node* AVL::LRRotation(Node *p) {
    return nullptr;
}

Node* AVL::RLRotation(Node *p) {
    return nullptr;
}

Node* AVL::rInsert(Node *p, int key) {
    Node* t;
    if (p == nullptr){
        t = new Node;
        t->data = key;
        t->lchild = nullptr;
        t->rchild = nullptr;
        t->height = 1;  // Starting height from 1 onwards instead of 0
        return t;
    }

    if (key < p->data){
        p->lchild = rInsert(p->lchild, key);
    } else if (key > p->data){
        p->rchild = rInsert(p->rchild, key);
    }

    // Update height
    p->height = NodeHeight(p);

    // Balance Factor and Rotation
    if (BalanceFactor(p) == 2 && BalanceFactor(p->lchild) == 1) {
        return LLRotation(p);
    } else if (BalanceFactor(p) == 2 && BalanceFactor(p->lchild) == -1){
        return LRRotation(p);
    } else if (BalanceFactor(p) == -2 && BalanceFactor(p->rchild) == -1){
        return RRRotation(p);
    } else if (BalanceFactor(p) == -2 && BalanceFactor(p->rchild) == 1){
        return RLRotation(p);
    }

    return p;
}

void AVL::Inorder(Node *p) {
    if (p){
        Inorder(p->lchild);
        cout << p->data << ", " << flush;
        Inorder(p->rchild);
    }
}


int main() {

    // LL Rotation
    AVL tll;
    tll.root = tll.rInsert(tll.root, 30);
    tll.root = tll.rInsert(tll.root, 20);
    tll.root = tll.rInsert(tll.root, 10);

    tll.Inorder();
    cout << endl;

    // RR Rotation
    AVL trr;
    trr.root = trr.rInsert(trr.root, 10);
    trr.root = trr.rInsert(trr.root, 20);
    trr.root = trr.rInsert(trr.root, 30);

    trr.Inorder();
    cout << endl;

    return 0;
}

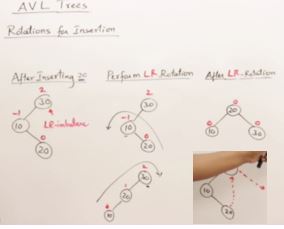
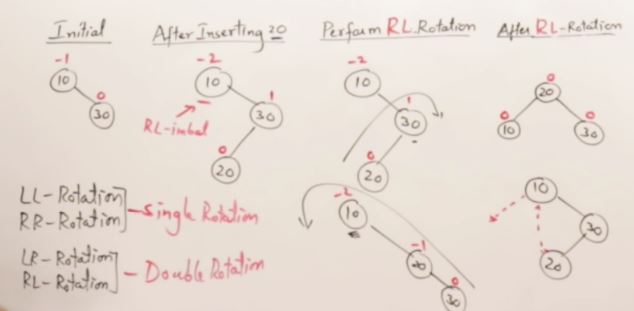
LR and RL Rotation on AVL

#include <iostream>

using namespace std;

class Node {
public:
    Node* lchild;
    int data;
    Node* rchild;
    int height;
};

class AVL{
public:
    Node* root;

    AVL(){ root = nullptr; }

    // Helper methods for inserting
    int NodeHeight(Node* p);
    int BalanceFactor(Node* p);
    Node* LLRotation(Node* p);
    Node* RRRotation(Node* p);
    Node* LRRotation(Node* p);
    Node* RLRotation(Node* p);

    // Insert
    Node* rInsert(Node* p, int key);

    // Traversal
    void Inorder(Node* p);
    void Inorder(){ Inorder(root); }
    Node* getRoot(){ return root; }
};

int AVL::NodeHeight(Node *p) {
    int hl;
    int hr;

    hl = (p && p->lchild) ? p->lchild->height : 0;
    hr = (p && p->rchild) ? p->rchild->height : 0;

    return hl > hr ? hl + 1 : hr + 1;
}

int AVL::BalanceFactor(Node *p) {
    int hl;
    int hr;

    hl = (p && p->lchild) ? p->lchild->height : 0;
    hr = (p && p->rchild) ? p->rchild->height : 0;

    return hl - hr;
}

Node* AVL::LLRotation(Node *p) {
    Node* pl = p->lchild;
    Node* plr = pl->rchild;

    pl->rchild = p;
    p->lchild = plr;

    // Update height
    p->height = NodeHeight(p);
    pl->height = NodeHeight(pl);

    // Update root
    if (root == p){
        root = pl;
    }
    return pl;
}

Node* AVL::RRRotation(Node *p) {
    Node* pr = p->rchild;
    Node* prl = pr->lchild;

    pr->lchild = p;
    p->rchild = prl;

    // Update height
    p->height = NodeHeight(p);
    pr->height = NodeHeight(pr);

    // Update root
    if (root == p){
        root = pr;
    }
    return pr;
}

Node* AVL::LRRotation(Node *p) {
    Node* pl = p->lchild;
    Node* plr = pl->rchild;

    pl->rchild = plr->lchild;
    p->lchild = plr->rchild;

    plr->lchild = pl;
    plr->rchild = p;

    // Update height
    pl->height = NodeHeight(pl);
    p->height = NodeHeight(p);
    plr->height = NodeHeight(plr);

    // Update root
    if (p == root){
        root = plr;
    }
    return plr;
}

Node* AVL::RLRotation(Node *p) {
    Node* pr = p->rchild;
    Node* prl = pr->lchild;

    pr->lchild = prl->rchild;
    p->rchild =prl->lchild;

    prl->rchild = pr;
    prl->lchild = p;
    // Update height
    pr->height = NodeHeight(pr);
    p->height = NodeHeight(p);
    prl->height = NodeHeight(prl);

    // Update root
    if (root == p){
        root = prl;
    }
    return prl;
}

Node* AVL::rInsert(Node *p, int key) {
    Node* t;
    if (p == nullptr){
        t = new Node;
        t->data = key;
        t->lchild = nullptr;
        t->rchild = nullptr;
        t->height = 1;  // Starting height from 1 onwards instead of 0
        return t;
    }

    if (key < p->data){
        p->lchild = rInsert(p->lchild, key);
    } else if (key > p->data){
        p->rchild = rInsert(p->rchild, key);
    }

    // Update height
    p->height = NodeHeight(p);

    // Balance Factor and Rotation
    if (BalanceFactor(p) == 2 && BalanceFactor(p->lchild) == 1) {
        return LLRotation(p);
    } else if (BalanceFactor(p) == 2 && BalanceFactor(p->lchild) == -1){
        return LRRotation(p);
    } else if (BalanceFactor(p) == -2 && BalanceFactor(p->rchild) == -1){
        return RRRotation(p);
    } else if (BalanceFactor(p) == -2 && BalanceFactor(p->rchild) == 1){
        return RLRotation(p);
    }

    return p;
}

void AVL::Inorder(Node *p) {
    if (p){
        Inorder(p->lchild);
        cout << p->data << ", " << flush;
        Inorder(p->rchild);
    }
}


int main() {

    // LR Rotation
    AVL tll;
    tll.root = tll.rInsert(tll.root, 50);
    tll.root = tll.rInsert(tll.root, 10);
    tll.root = tll.rInsert(tll.root, 20);

    tll.Inorder();
    cout << endl;

    // RL Rotation
    AVL trr;
    trr.root = trr.rInsert(trr.root, 20);
    trr.root = trr.rInsert(trr.root, 50);
    trr.root = trr.rInsert(trr.root, 30);

    trr.Inorder();
    cout << endl;

    return 0;
}

Deletion From AVL tree with Rotations

#include <iostream>

using namespace std;

class Node {
public:
    Node* lchild;
    int data;
    Node* rchild;
    int height;
};

class AVL{
public:
    Node* root;

    AVL(){ root = nullptr; }

    // Helper methods for inserting/deleting
    int NodeHeight(Node* p);
    int BalanceFactor(Node* p);
    Node* LLRotation(Node* p);
    Node* RRRotation(Node* p);
    Node* LRRotation(Node* p);
    Node* RLRotation(Node* p);
    Node* InPre(Node* p);
    Node* InSucc(Node* p);

    // Insert
    Node* rInsert(Node* p, int key);

    // Traversal
    void Inorder(Node* p);
    void Inorder(){ Inorder(root); }
    Node* getRoot(){ return root; }

    // Delete
    Node* Delete(Node* p, int key);
};

int AVL::NodeHeight(Node *p) {
    int hl;
    int hr;

    hl = (p && p->lchild) ? p->lchild->height : 0;
    hr = (p && p->rchild) ? p->rchild->height : 0;

    return hl > hr ? hl + 1 : hr + 1;
}

int AVL::BalanceFactor(Node *p) {
    int hl;
    int hr;

    hl = (p && p->lchild) ? p->lchild->height : 0;
    hr = (p && p->rchild) ? p->rchild->height : 0;

    return hl - hr;
}

Node* AVL::LLRotation(Node *p) {
    Node* pl = p->lchild;
    Node* plr = pl->rchild;

    pl->rchild = p;
    p->lchild = plr;

    // Update height
    p->height = NodeHeight(p);
    pl->height = NodeHeight(pl);

    // Update root
    if (root == p){
        root = pl;
    }
    return pl;
}

Node* AVL::RRRotation(Node *p) {
    Node* pr = p->rchild;
    Node* prl = pr->lchild;

    pr->lchild = p;
    p->rchild = prl;

    // Update height
    p->height = NodeHeight(p);
    pr->height = NodeHeight(pr);

    // Update root
    if (root == p){
        root = pr;
    }
    return pr;
}

Node* AVL::LRRotation(Node *p) {
    Node* pl = p->lchild;
    Node* plr = pl->rchild;

    pl->rchild = plr->lchild;
    p->lchild = plr->rchild;

    plr->lchild = pl;
    plr->rchild = p;

    // Update height
    pl->height = NodeHeight(pl);
    p->height = NodeHeight(p);
    plr->height = NodeHeight(plr);

    // Update root
    if (p == root){
        root = plr;
    }
    return plr;
}

Node* AVL::RLRotation(Node *p) {
    Node* pr = p->rchild;
    Node* prl = pr->lchild;

    pr->lchild = prl->rchild;
    p->rchild = prl->lchild;

    prl->rchild = pr;
    prl->lchild = p;

    // Update height
    pr->height = NodeHeight(pr);
    p->height = NodeHeight(p);
    prl->height = NodeHeight(prl);

    // Update root
    if (root == p){
        root = prl;
    }
    return prl;
}

Node* AVL::InPre(Node *p) {
    while (p && p->rchild != nullptr){
        p = p->rchild;
    }
    return p;
}

Node* AVL::InSucc(Node *p) {
    while (p && p->lchild != nullptr){
        p = p->lchild;
    }
    return p;
}

Node* AVL::rInsert(Node *p, int key) {
    Node* t;
    if (p == nullptr){
        t = new Node;
        t->data = key;
        t->lchild = nullptr;
        t->rchild = nullptr;
        t->height = 1;  // Starting height from 1 onwards instead of 0
        return t;
    }

    if (key < p->data){
        p->lchild = rInsert(p->lchild, key);
    } else if (key > p->data){
        p->rchild = rInsert(p->rchild, key);
    }

    // Update height
    p->height = NodeHeight(p);

    // Balance Factor and Rotation
    if (BalanceFactor(p) == 2 && BalanceFactor(p->lchild) == 1) {
        return LLRotation(p);
    } else if (BalanceFactor(p) == 2 && BalanceFactor(p->lchild) == -1){
        return LRRotation(p);
    } else if (BalanceFactor(p) == -2 && BalanceFactor(p->rchild) == -1){
        return RRRotation(p);
    } else if (BalanceFactor(p) == -2 && BalanceFactor(p->rchild) == 1){
        return RLRotation(p);
    }

    return p;
}

void AVL::Inorder(Node *p) {
    if (p){
        Inorder(p->lchild);
        cout << p->data << ", " << flush;
        Inorder(p->rchild);
    }
}

Node* AVL::Delete(Node *p, int key) {
    if (p == nullptr){
        return nullptr;
    }

    if (p->lchild == nullptr && p->rchild == nullptr){
        if (p == root){
            root = nullptr;
        }
        delete p;
        return nullptr;
    }

    if (key < p->data){
        p->lchild = Delete(p->lchild, key);
    } else if (key > p->data){
        p->rchild = Delete(p->rchild, key);
    } else {
        Node* q;
        if (NodeHeight(p->lchild) > NodeHeight(p->rchild)){
            q = InPre(p->lchild);
            p->data = q->data;
            p->lchild = Delete(p->lchild, q->data);
        } else {
            q = InSucc(p->rchild);
            p->data = q->data;
            p->rchild = Delete(p->rchild, q->data);
        }
    }

    // Update height
    p->height = NodeHeight(p);

    // Balance Factor and Rotation
    if (BalanceFactor(p) == 2 && BalanceFactor(p->lchild) == 1) {  // L1 Rotation
        return LLRotation(p);
    } else if (BalanceFactor(p) == 2 && BalanceFactor(p->lchild) == -1){  // L-1 Rotation
        return LRRotation(p);
    } else if (BalanceFactor(p) == -2 && BalanceFactor(p->rchild) == -1){  // R-1 Rotation
        return RRRotation(p);
    } else if (BalanceFactor(p) == -2 && BalanceFactor(p->rchild) == 1){  // R1 Rotation
        return RLRotation(p);
    } else if (BalanceFactor(p) == 2 && BalanceFactor(p->lchild) == 0){  // L0 Rotation
        return LLRotation(p);
    } else if (BalanceFactor(p) == -2 && BalanceFactor(p->rchild) == 0){  // R0 Rotation
        return RRRotation(p);
    }

    return p;
}


int main() {

    AVL tree;

    int A[] = {10, 20, 30, 25, 28, 27, 5};
    for (int i=0; i<sizeof(A)/sizeof(A[0]); i++){
        tree.root = tree.rInsert(tree.root, A[i]);
    }

    tree.Inorder();
    cout << endl;

    tree.Delete(tree.root, 28);

    tree.Inorder();
    cout << endl;

    return 0;
}

Comment  Read more

26. Binary Search Trees

19 Jun 2020 | Algorithm

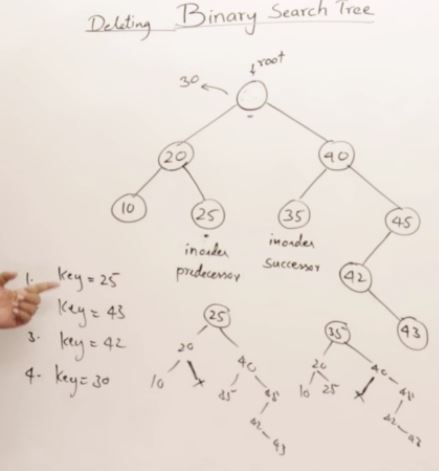
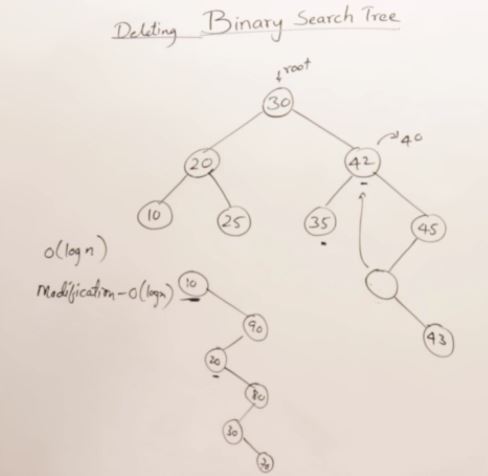
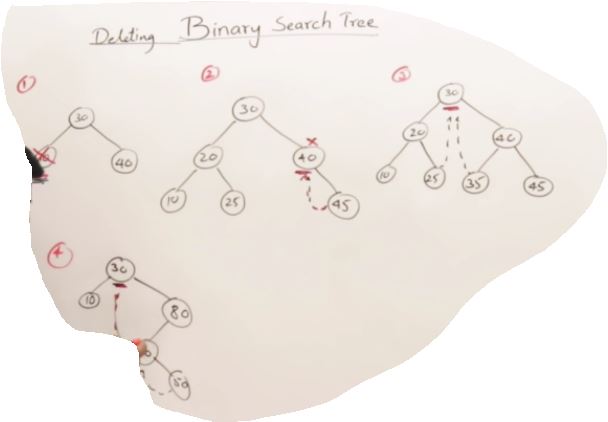
Binary Search Tree

#include <iostream>

using namespace std;
class Node
{
public:
    int data;
    Node* rchild;
    Node* lchild;

};
class BST
{
public:
    BST(){root=nullptr;}
    ~BST(){}
    void Insert(int key);
    void Inorder(){ Inorder(root);}
    void Inorder(Node* p);
    Node* Search(int key);
private:
    Node* root;
};
Node* BST::Search(int key)
{
    Node* p = root;
    while(p!= nullptr)
    {
        if(key == p->data)
        {
            return p;
        }
        else if(key<p->data)
        {
            p=p->lchild;
        }
        else
        {
            p=p->rchild;
        }

    }
    return nullptr;

}
void BST::Inorder(Node* p)
{
    if(p!=nullptr)
    {
        Inorder(p->lchild);
        cout<< p->data << " ";
        Inorder(p->rchild);
    }
}
void BST::Insert(int key)
{
    Node* p = root;
    Node* t;
    Node* r;

    if(root==nullptr)
    {
        t = new Node;
        t->data = key;
        t->lchild =nullptr;
        t->rchild =nullptr;
        root = t;
        return;
    }
    while(p!=nullptr)
    {
        r = p; // lastest pointer point to last indicated point
        if(key<p->data)
        {
            p = p->lchild;
        }
        else if(key > p->data)
        {
            p = p->rchild;
        }
    }

    t = new Node;
    t->data = key;
    t->lchild =nullptr;
    t->rchild =nullptr;
    if(key<r->data)
        r->lchild = t;
    if(key>r->data)
        r->rchild = t;
}

int main()
{
    BST bst;
    bst.Insert(10);
    bst.Insert(5);
    bst.Insert(20);
    bst.Insert(8);
    bst.Insert(30);

    //Inorder Traversal
    bst.Inorder();
    cout<<endl;

    // Search
    Node* Search_result;
    Search_result = bst.Search(5);
    if(Search_result!=nullptr)
    {
        cout << Search_result->data;
    }
    else
    {
        cout << "not found";
    }
    return 0;
}

Recursive Inset and Delete on BST

#include <iostream>

using namespace std;
class Node
{
public:
    int data;
    Node* rchild;
    Node* lchild;

};
class BST
{
public:
    BST(){root=nullptr;}
    ~BST(){}
    void Insert(int key);
    void Inorder(){ Inorder(root);}
    void Inorder(Node* p);
    Node* Search(int key);
    Node* preorder(){ preorder(root);}
    Node* preorder(Node* p);
    Node* Delete(Node* p,int key);
    Node* getRoot();
    int height(Node* p);
    Node* Insucc(Node* p);
private:
    Node* root;
};
int BST::height(Node* p)
{
    int x;
    int y;
    if(p==nullptr)
        return 0;
    x = height(p->lchild);
    y = height(p->rchild);
    return x>y?x+1:y+1;
}
Node* BST::getRoot()
{
    return root;
}
Node* BST::preorder(Node* p)
{
    while(p && p->rchild!=nullptr)
    {
        p=p->rchild;
    }
    cout<<" InPre : "<< p->data<<endl;
    return p;
}
Node* BST::Search(int key)
{
    Node* p = root;
    while(p!= nullptr)
    {
        if(key == p->data)
        {
            return p;
        }
        else if(key<p->data)
        {
            p=p->lchild;
        }
        else
        {
            p=p->rchild;
        }

    }
    return nullptr;

}
void BST::Inorder(Node* p)
{
    if(p!=nullptr)
    {
        Inorder(p->lchild);
        cout<< p->data << " ";
        Inorder(p->rchild);
    }
}
void BST::Insert(int key)
{
    Node* p = root;
    Node* t;
    Node* r;

    if(root==nullptr)
    {
        t = new Node;
        t->data = key;
        t->lchild =nullptr;
        t->rchild =nullptr;
        root = t;
        return;
    }
    while(p!=nullptr)
    {
        r = p; // lastest pointer point to last indicated point
        if(key<p->data)
        {
            p = p->lchild;
        }
        else if(key > p->data)
        {
            p = p->rchild;
        }
    }

    t = new Node;
    t->data = key;
    t->lchild =nullptr;
    t->rchild =nullptr;
    if(key<r->data)
        r->lchild = t;
    if(key>r->data)
        r->rchild = t;
}
Node* BST::Delete(Node* p,int key)
{
    Node* q;
    if(p==nullptr)
    {
        return nullptr;
    }

    if(p->lchild==nullptr&&p->rchild==nullptr)
    {
        if(p==root)
        {
            root=nullptr;
        }
        delete p;
        return nullptr;
    }
    if(key<p->data)
    {
        p->lchild = Delete(p->lchild,key);
    }
    else if(key>p->data)
    {
        p->rchild = Delete(p->rchild,key);
    }
    else
    {
        if(height(p->lchild)>height(p->rchild))
        {
            q = preorder(p->lchild);
            p->data = q->data;
            p->lchild = Delete(p->lchild, q->data);
        }
        else
        {
            q = Insucc(p->rchild);
            p->data = q->data;
            p->rchild = Delete(p->rchild, q->data);
        }
    }
    return p;
}
Node* BST::Insucc(Node *p) {
    while (p && p->lchild != nullptr){
        p = p->lchild;
    }
    cout<< "InSucc: "<<p->data<<endl;
    return p;
}
int main()
{
    BST bst;
    bst.Insert(10);
    bst.Insert(5);
    bst.Insert(20);
    bst.Insert(8);
    bst.Insert(30);

    //Inorder Traversal
    bst.Inorder();
    cout<<endl;

    // Preoder
    bst.preorder();
    cout<<endl;


    // Search
    Node* Search_result;
    Search_result = bst.Search(5);
    if(Search_result!=nullptr)
    {
        cout << Search_result->data<<endl;;
    }
    else
    {
        cout << "not found";
    }
    // Delete
    bst.Delete(bst.getRoot(),20);
    bst.Inorder();
    cout<<endl;
    return 0;
}

Generating BST from Preorder.

#include <iostream>
#include <stack>

using namespace std;
class Node
{
public:
    int data;
    Node* rchild;
    Node* lchild;

};
class BST
{
public:
    BST(){root=nullptr;}
    ~BST(){}
    void Insert(int key);
    void Inorder(){ Inorder(root);}
    void Inorder(Node* p);
    Node* Search(int key);
    Node* preorder(){ preorder(root);}
    Node* preorder(Node* p);
    Node* Delete(Node* p,int key);
    Node* getRoot();
    int height(Node* p);
    Node* Insucc(Node* p);
    void createFromPreorder(int pre[], int size_);
private:
    Node* root;
};
void BST::createFromPreorder(int pre[], int size_)
{
    //Create root node
    int i = 0;
    root = new Node;
    root->data = pre[i++];
    root->lchild = nullptr;
    root->rchild = nullptr;

    // iteratives steps
    Node* t;
    Node* p = root;
    stack <Node*> stk;

    while(i<size_)
    {
        //left child case
        if(pre[i]<p->data)
        {
            t = new Node;
            t->data = pre[i++];
            t->lchild =nullptr;
            t->rchild =nullptr;
            p->lchild =t;
            stk.push(p);
            p = t;
        }
        else
        {
            //Right child case
            if(pre[i]>p->data && pre[i]<stk.empty()?32767:stk.top()->data)
            {
                t = new Node;
                t->data = pre[i++];
                t->lchild = nullptr;
                t->rchild = nullptr;
                p->rchild = t;
                p = t;
            }
            else
            {
                p = stk.top();
                stk.pop();
            }

        }
    }

}
int BST::height(Node* p)
{
    int x;
    int y;
    if(p==nullptr)
        return 0;
    x = height(p->lchild);
    y = height(p->rchild);
    return x>y?x+1:y+1;
}
Node* BST::getRoot()
{
    return root;
}
Node* BST::preorder(Node* p)
{
    while(p && p->rchild!=nullptr)
    {
        p=p->rchild;
    }
    cout<<" InPre : "<< p->data<<endl;
    return p;
}
Node* BST::Search(int key)
{
    Node* p = root;
    while(p!= nullptr)
    {
        if(key == p->data)
        {
            return p;
        }
        else if(key<p->data)
        {
            p=p->lchild;
        }
        else
        {
            p=p->rchild;
        }

    }
    return nullptr;

}
void BST::Inorder(Node* p)
{
    if(p!=nullptr)
    {
        Inorder(p->lchild);
        cout<< p->data << " ";
        Inorder(p->rchild);
    }
}
void BST::Insert(int key)
{
    Node* p = root;
    Node* t;
    Node* r;

    if(root==nullptr)
    {
        t = new Node;
        t->data = key;
        t->lchild =nullptr;
        t->rchild =nullptr;
        root = t;
        return;
    }
    while(p!=nullptr)
    {
        r = p; // lastest pointer point to last indicated point
        if(key<p->data)
        {
            p = p->lchild;
        }
        else if(key > p->data)
        {
            p = p->rchild;
        }
    }

    t = new Node;
    t->data = key;
    t->lchild =nullptr;
    t->rchild =nullptr;
    if(key<r->data)
        r->lchild = t;
    if(key>r->data)
        r->rchild = t;
}
Node* BST::Delete(Node* p,int key)
{
    Node* q;
    if(p==nullptr)
    {
        return nullptr;
    }

    if(p->lchild==nullptr&&p->rchild==nullptr)
    {
        if(p==root)
        {
            root=nullptr;
        }
        delete p;
        return nullptr;
    }
    if(key<p->data)
    {
        p->lchild = Delete(p->lchild,key);
    }
    else if(key>p->data)
    {
        p->rchild = Delete(p->rchild,key);
    }
    else
    {
        if(height(p->lchild)>height(p->rchild))
        {
            q = preorder(p->lchild);
            p->data = q->data;
            p->lchild = Delete(p->lchild, q->data);
        }
        else
        {
            q = Insucc(p->rchild);
            p->data = q->data;
            p->rchild = Delete(p->rchild, q->data);
        }
    }
    return p;
}
Node* BST::Insucc(Node *p) {
    while (p && p->lchild != nullptr){
        p = p->lchild;
    }
    cout<< "InSucc: "<<p->data<<endl;
    return p;
}
int main()
{
    BST bst;
    bst.Insert(10);
    bst.Insert(5);
    bst.Insert(20);
    bst.Insert(8);
    bst.Insert(30);

    //Inorder Traversal
    bst.Inorder();
    cout<<endl;

    // Preoder
    bst.preorder();
    cout<<endl;


    // Search
    Node* Search_result;
    Search_result = bst.Search(5);
    if(Search_result!=nullptr)
    {
        cout << Search_result->data<<endl;;
    }
    else
    {
        cout << "not found";
    }
    // Delete
    bst.Delete(bst.getRoot(),20);
    bst.Inorder();
    cout<<endl;

    // BST from Preorder Traversal
    cout << "BST from Preorder: " << flush;
    int pre[] = {30, 20, 10, 15, 25, 40, 50, 45};
    int n = sizeof(pre)/sizeof(pre[0]);

    BST b;
    b.createFromPreorder(pre,n);
    b.Inorder();
    return 0;
}

Quiz

Comment  Read more

25. Trees 3(Code)

19 Jun 2020 | Algorithm

Generate Tree From Traversals

#include <iostream>
#include <queue>
#include <stack>

using namespace std;

class Node{
public:
    Node* lchild;
    int data;
    Node* rchild;
    Node() {};
    Node(int data);
};

Node::Node(int data) {
    lchild = nullptr;
    this->data = data;
    rchild = nullptr;
}

class Tree{
private:
    Node* root;
public:
    Tree();
    ~Tree();
    void CreateTree();
    void Preorder(Node* p);
    void Preorder() { Preorder(root); }  // Passing Private Parameter in Constructor
    void Inorder(Node* p);
    void Inorder() { Inorder(root); }
    void Postorder(Node* p);
    void Postorder() { Postorder(root); }
    void Levelorder(Node* p);
    void Levelorder() { Levelorder(root); }
    int Height(Node* p);
    int Height() { return Height(root); }
    void iterativePreorder(Node* p);
    void iterativePreorder() { iterativePreorder(root); }
    void iterativeInorder(Node* p);
    void iterativeInorder() { iterativeInorder(root); }
    void iterativePostorder(Node* p);
    void iterativePostorder() { iterativePostorder(root); }
    Node* generateFromTraversal(int inorder[], int preorder[], int inStart, int inEnd);
};

Tree::Tree() {
    root = nullptr;
}

Tree::~Tree() {
    // TODO
}

void Tree::CreateTree() {
    Node* p;
    Node* t;
    int x;
    queue<Node*> q;

    root = new Node;
    cout << "Enter root data: " << flush;
    cin >> x;
    root->data = x;
    root->lchild = nullptr;
    root->rchild = nullptr;  
    q.emplace(root);

    while (! q.empty()){
        p = q.front();
        q.pop();

        cout << "Enter left child data of " << p->data << ": " << flush;
        cin >> x;
        if (x != -1){
            t = new Node;
            t->data = x;
            t->lchild = nullptr;
            t->rchild = nullptr;
            p->lchild = t;
            q.emplace(t);
        }

        cout << "Enter right child data of " << p->data << ": " << flush;
        cin >> x;
        if (x != -1){
            t = new Node;
            t->data = x;
            t->lchild = nullptr;
            t->rchild = nullptr;
            p->rchild = t;
            q.emplace(t);
        }
    }
}

void Tree::Preorder(Node *p) {
    if (p){
        cout << p->data << ", " << flush;
        Preorder(p->lchild);
        Preorder(p->rchild);
    }
}

void Tree::Inorder(Node *p) {
    if (p){
        Inorder(p->lchild);
        cout << p->data << ", " << flush;
        Inorder(p->rchild);
    }
}

void Tree::Postorder(Node *p) {
    if (p){
        Postorder(p->lchild);
        Postorder(p->rchild);
        cout << p->data << ", " << flush;
    }
}

void Tree::Levelorder(Node *p) {
    queue<Node*> q;
    cout << p->data << ", " << flush;
    q.emplace(p);

    while (! q.empty()){
        p = q.front();
        q.pop();

        if (p->lchild){
            cout << p->lchild->data << ", " << flush;
            q.emplace(p->lchild);
        }

        if (p->rchild){
            cout << p->rchild->data << ", " << flush;
            q.emplace(p->rchild);
        }
    }
}

int Tree::Height(Node *p) {
    int l = 0;
    int r = 0;
    if (p == nullptr){
        return 0;
    }

    l = Height(p->lchild);
    r = Height(p->rchild);

    if (l > r){
        return l + 1;
    } else {
        return r + 1;
    }
}

void Tree::iterativePreorder(Node *p) {
    stack<Node*> stk;
    while (p != nullptr || ! stk.empty()){
        if (p != nullptr){
            cout << p->data << ", " << flush;
            stk.emplace(p);
            p = p->lchild;
        } else {
            p = stk.top();
            stk.pop();
            p = p->rchild;
        }
    }
    cout << endl;
}

void Tree::iterativeInorder(Node *p) {
    stack<Node*> stk;
    while (p != nullptr || ! stk.empty()){
        if (p != nullptr){
            stk.emplace(p);
            p = p->lchild;
        } else {
            p = stk.top();
            stk.pop();
            cout << p->data << ", " << flush;
            p = p->rchild;
        }
    }
    cout << endl;
}

void Tree::iterativePostorder(Node *p) {
    stack<long int> stk;
    long int temp;
    while (p != nullptr || ! stk.empty()){
        if (p != nullptr){
            stk.emplace((long int)p);
            p = p->lchild;
        } else {
            temp = stk.top();
            stk.pop();
            if (temp > 0){
                stk.emplace(-temp);
                p = ((Node*)temp)->rchild;
            } else {
                cout << ((Node*)(-1 * temp))->data << ", " << flush;
                p = nullptr;
            }
        }
    }
    cout << endl;
}

int searchInorder(int inArray[], int inStart, int inEnd, int data){
    for (int i=inStart; i<=inEnd; i++){
        if (inArray[i] == data){
            return i;
        }
    }
    return -1;
}

Node* Tree::generateFromTraversal(int *inorder, int *preorder, int inStart, int inEnd) {
    // Reference: https://algorithms.tutorialhorizon.com/make-a-binary-tree-from-given-inorder-and-preorder-traveral/
    static int preIndex = 0;

    if (inStart > inEnd){
        return nullptr;
    }

    Node* node = new Node(preorder[preIndex++]);

    if (inStart == inEnd){
        return node;
    }

    int splitIndex = searchInorder(inorder, inStart, inEnd, node->data);
    node->lchild = generateFromTraversal(inorder, preorder, inStart, splitIndex-1);
    node->rchild = generateFromTraversal(inorder, preorder, splitIndex+1, inEnd);

    return node;
}


int main() {

    Tree bt;

    int preorder[] = {4, 7, 9, 6, 3, 2, 5, 8, 1};
    int inorder[] = {7, 6, 9, 3, 4, 5, 8, 2, 1};


    Node* T = bt.generateFromTraversal(inorder, preorder, 0, sizeof(inorder)/sizeof(inorder[0])-1);
    bt.Preorder(T);

    return 0;
}

Height and Count of Binary Tree

#include <iostream>
#include <queue>
#include <stack>

using namespace std;

class Node{
public:
    Node* lchild;
    int data;
    Node* rchild;
    Node() {};
    Node(int data);
};

Node::Node(int data) {
    lchild = nullptr;
    this->data = data;
    rchild = nullptr;
}

class Tree{
private:
    Node* root;
public:
    Tree();
    ~Tree();
    void CreateTree();
    void Preorder(Node* p);
    void Preorder() { Preorder(root); }  // Passing Private Parameter in Constructor
    void Inorder(Node* p);
    void Inorder() { Inorder(root); }
    void Postorder(Node* p);
    void Postorder() { Postorder(root); }
    void Levelorder(Node* p);
    void Levelorder() { Levelorder(root); }
    int Height(Node* p);
    int Height() { return Height(root); }
    void iterativePreorder(Node* p);
    void iterativePreorder() { iterativePreorder(root); }
    void iterativeInorder(Node* p);
    void iterativeInorder() { iterativeInorder(root); }
    void iterativePostorder(Node* p);
    void iterativePostorder() { iterativePostorder(root); }
    Node* generateFromTraversal(int inorder[], int preorder[], int inStart, int inEnd);
    int Count(Node* p);
    int sum(Node* p);
    int deg2NodeCount(Node* p);
};
int Tree::deg2NodeCount(Node* p)
{
    int x,y;
    if(p!=nullptr)
    {
        x = deg2NodeCount(p->lchild);
        y = deg2NodeCount(p->rchild);
        if(p->lchild&&p->rchild)
        {
            return x+y+1;
        }
        else
        {
            return x+y;
        }
    }
    return 0;
}
int Tree::sum(Node* p)
{
    int x,y;
    if(p!=nullptr)
    {
        x = sum(p->lchild);
        y = sum(p->rchild);
        return x+y+p->data;
    }
    return 0;
}

int Tree::Count(Node* p)
{
    int x;
    int y;
    if(p!=nullptr)
    {
        x = Count(p->lchild);
        y = Count(p->rchild);
        return x+y+1;
    }
    return 0;

}

Tree::Tree() {
    root = nullptr;
}

Tree::~Tree() {
    // TODO
}

void Tree::CreateTree() {
    Node* p;
    Node* t;
    int x;
    queue<Node*> q;

    root = new Node;
    cout << "Enter root data: " << flush;
    cin >> x;
    root->data = x;
    root->lchild = nullptr;
    root->rchild = nullptr;
    q.emplace(root);

    while (! q.empty()){
        p = q.front();
        q.pop();

        cout << "Enter left child data of " << p->data << ": " << flush;
        cin >> x;
        if (x != -1){
            t = new Node;
            t->data = x;
            t->lchild = nullptr;
            t->rchild = nullptr;
            p->lchild = t;
            q.emplace(t);
        }

        cout << "Enter right child data of " << p->data << ": " << flush;
        cin >> x;
        if (x != -1){
            t = new Node;
            t->data = x;
            t->lchild = nullptr;
            t->rchild = nullptr;
            p->rchild = t;
            q.emplace(t);
        }
    }
}

void Tree::Preorder(Node *p) {
    if (p){
        cout << p->data << ", " << flush;
        Preorder(p->lchild);
        Preorder(p->rchild);
    }
}

void Tree::Inorder(Node *p) {
    if (p){
        Inorder(p->lchild);
        cout << p->data << ", " << flush;
        Inorder(p->rchild);
    }
}

void Tree::Postorder(Node *p) {
    if (p){
        Postorder(p->lchild);
        Postorder(p->rchild);
        cout << p->data << ", " << flush;
    }
}

void Tree::Levelorder(Node *p) {
    queue<Node*> q;
    cout << p->data << ", " << flush;
    q.emplace(p);

    while (! q.empty()){
        p = q.front();
        q.pop();

        if (p->lchild){
            cout << p->lchild->data << ", " << flush;
            q.emplace(p->lchild);
        }

        if (p->rchild){
            cout << p->rchild->data << ", " << flush;
            q.emplace(p->rchild);
        }
    }
}

int Tree::Height(Node *p) {
    int l = 0;
    int r = 0;
    if (p == nullptr){
        return 0;
    }

    l = Height(p->lchild);
    r = Height(p->rchild);

    if (l > r){
        return l + 1;
    } else {
        return r + 1;
    }
}

void Tree::iterativePreorder(Node *p) {
    stack<Node*> stk;
    while (p != nullptr || ! stk.empty()){
        if (p != nullptr){
            cout << p->data << ", " << flush;
            stk.emplace(p);
            p = p->lchild;
        } else {
            p = stk.top();
            stk.pop();
            p = p->rchild;
        }
    }
    cout << endl;
}

void Tree::iterativeInorder(Node *p) {
    stack<Node*> stk;
    while (p != nullptr || ! stk.empty()){
        if (p != nullptr){
            stk.emplace(p);
            p = p->lchild;
        } else {
            p = stk.top();
            stk.pop();
            cout << p->data << ", " << flush;
            p = p->rchild;
        }
    }
    cout << endl;
}

void Tree::iterativePostorder(Node *p) {
    stack<long int> stk;
    long int temp;
    while (p != nullptr || ! stk.empty()){
        if (p != nullptr){
            stk.emplace((long int)p);
            p = p->lchild;
        } else {
            temp = stk.top();
            stk.pop();
            if (temp > 0){
                stk.emplace(-temp);
                p = ((Node*)temp)->rchild;
            } else {
                cout << ((Node*)(-1 * temp))->data << ", " << flush;
                p = nullptr;
            }
        }
    }
    cout << endl;
}

int searchInorder(int inArray[], int inStart, int inEnd, int data){
    for (int i=inStart; i<=inEnd; i++){
        if (inArray[i] == data){
            return i;
        }
    }
    return -1;
}

Node* Tree::generateFromTraversal(int *inorder, int *preorder, int inStart, int inEnd) {
    // Reference: https://algorithms.tutorialhorizon.com/make-a-binary-tree-from-given-inorder-and-preorder-traveral/
    static int preIndex = 0;

    if (inStart > inEnd){
        return nullptr;
    }

    Node* node = new Node(preorder[preIndex++]);

    if (inStart == inEnd){
        return node;
    }

    int splitIndex = searchInorder(inorder, inStart, inEnd, node->data);
    node->lchild = generateFromTraversal(inorder, preorder, inStart, splitIndex-1);
    node->rchild = generateFromTraversal(inorder, preorder, splitIndex+1, inEnd);

    return node;
}


int main() {

    Tree bt;

    int preorder[] = {4, 7, 9, 6, 3, 2, 5, 8, 1};
    int inorder[] = {7, 6, 9, 3, 4, 5, 8, 2, 1};


    Node* T = bt.generateFromTraversal(inorder, preorder, 0, sizeof(inorder)/sizeof(inorder[0])-1);
    bt.Preorder(T);
    cout<<endl;

    cout << "Heigh :" << bt.Height(T)<<endl;
    cout << "Count :" << bt.Count(T)<<endl;
    cout << "Sum: " << bt.sum(T) << endl;
    cout << "# of degree 2 nodes: " << bt.deg2NodeCount(T) << endl;

    return 0;
}

Count Leaf Nodes of a Binary

#include <iostream>
#include <queue>
#include <stack>

using namespace std;

class Node{
public:
    Node* lchild;
    int data;
    Node* rchild;
    Node() {};
    Node(int data);
};

Node::Node(int data) {
    lchild = nullptr;
    this->data = data;
    rchild = nullptr;
}

class Tree{
private:
    Node* root;
public:
    Tree();
    ~Tree();
    void CreateTree();
    void Preorder(Node* p);
    void Preorder() { Preorder(root); }  // Passing Private Parameter in Constructor
    void Inorder(Node* p);
    void Inorder() { Inorder(root); }
    void Postorder(Node* p);
    void Postorder() { Postorder(root); }
    void Levelorder(Node* p);
    void Levelorder() { Levelorder(root); }
    int Height(Node* p);
    int Height() { return Height(root); }
    void iterativePreorder(Node* p);
    void iterativePreorder() { iterativePreorder(root); }
    void iterativeInorder(Node* p);
    void iterativeInorder() { iterativeInorder(root); }
    void iterativePostorder(Node* p);
    void iterativePostorder() { iterativePostorder(root); }
    Node* generateFromTraversal(int inorder[], int preorder[], int inStart, int inEnd);
    int Count(Node* p);
    int sum(Node* p);
    int deg2NodeCount(Node* p);
    int leafNodeCount(Node* p);
    int deg1ordeg2NodeCount(Node* p);
    int deg1NodeCount(Node* p);
    void DestroyTree(Node *p);
};
void Tree::DestroyTree(Node *p)
{
    if(p!=nullptr)
    {
        DestroyTree(p->lchild);
        DestroyTree(p->rchild);
        delete p;
    }
}
int Tree::deg1NodeCount(Node* p)
{
    int x,y;
    if(p!=nullptr)
    {
        x = deg1NodeCount(p->lchild);
        y = deg1NodeCount(p->rchild);
        if(p->lchild!=nullptr ^ p->rchild != nullptr)
        {
            return x+y+1;
        }
        else
        {
            return x+y;
        }
    }
    return 0;
}
int Tree::deg1ordeg2NodeCount(Node* p)
{
    int x;
    int y;
    if(p!=nullptr)
    {
        x= deg1ordeg2NodeCount(p->lchild);
        y= deg1ordeg2NodeCount(p->rchild);
        if(p->lchild != nullptr || p->rchild!=nullptr)
        {
            return x+y+1;
        }
        else
        {
            return x+y;
        }

    }
}
int Tree::leafNodeCount(Node* p)
{
    int x, y;
    if(p!=nullptr)
    {
        x = leafNodeCount(p->lchild);
        y = leafNodeCount(p->rchild);
        if(p->lchild == nullptr && p->rchild == nullptr)
        {
            return x+y+1;
        }
        else
        {
            return x+y;
        }

    }
    return 0;
}
int Tree::deg2NodeCount(Node* p)
{
    int x,y;
    if(p!=nullptr)
    {
        x = deg2NodeCount(p->lchild);
        y = deg2NodeCount(p->rchild);
        if(p->lchild&&p->rchild)
        {
            return x+y+1;
        }
        else
        {
            return x+y;
        }
    }
    return 0;
}
int Tree::sum(Node* p)
{
    int x,y;
    if(p!=nullptr)
    {
        x = sum(p->lchild);
        y = sum(p->rchild);
        return x+y+p->data;
    }
    return 0;
}

int Tree::Count(Node* p)
{
    int x;
    int y;
    if(p!=nullptr)
    {
        x = Count(p->lchild);
        y = Count(p->rchild);
        return x+y+1;
    }
    return 0;

}

Tree::Tree() {
    root = nullptr;
}

Tree::~Tree() {
    // TODO
}

void Tree::CreateTree() {
    Node* p;
    Node* t;
    int x;
    queue<Node*> q;

    root = new Node;
    cout << "Enter root data: " << flush;
    cin >> x;
    root->data = x;
    root->lchild = nullptr;
    root->rchild = nullptr;
    q.emplace(root);

    while (! q.empty()){
        p = q.front();
        q.pop();

        cout << "Enter left child data of " << p->data << ": " << flush;
        cin >> x;
        if (x != -1){
            t = new Node;
            t->data = x;
            t->lchild = nullptr;
            t->rchild = nullptr;
            p->lchild = t;
            q.emplace(t);
        }

        cout << "Enter right child data of " << p->data << ": " << flush;
        cin >> x;
        if (x != -1){
            t = new Node;
            t->data = x;
            t->lchild = nullptr;
            t->rchild = nullptr;
            p->rchild = t;
            q.emplace(t);
        }
    }
}

void Tree::Preorder(Node *p) {
    if (p){
        cout << p->data << ", " << flush;
        Preorder(p->lchild);
        Preorder(p->rchild);
    }
}

void Tree::Inorder(Node *p) {
    if (p){
        Inorder(p->lchild);
        cout << p->data << ", " << flush;
        Inorder(p->rchild);
    }
}

void Tree::Postorder(Node *p) {
    if (p){
        Postorder(p->lchild);
        Postorder(p->rchild);
        cout << p->data << ", " << flush;
    }
}

void Tree::Levelorder(Node *p) {
    queue<Node*> q;
    cout << p->data << ", " << flush;
    q.emplace(p);

    while (! q.empty()){
        p = q.front();
        q.pop();

        if (p->lchild){
            cout << p->lchild->data << ", " << flush;
            q.emplace(p->lchild);
        }

        if (p->rchild){
            cout << p->rchild->data << ", " << flush;
            q.emplace(p->rchild);
        }
    }
}

int Tree::Height(Node *p) {
    int l = 0;
    int r = 0;
    if (p == nullptr){
        return 0;
    }

    l = Height(p->lchild);
    r = Height(p->rchild);

    if (l > r){
        return l + 1;
    } else {
        return r + 1;
    }
}

void Tree::iterativePreorder(Node *p) {
    stack<Node*> stk;
    while (p != nullptr || ! stk.empty()){
        if (p != nullptr){
            cout << p->data << ", " << flush;
            stk.emplace(p);
            p = p->lchild;
        } else {
            p = stk.top();
            stk.pop();
            p = p->rchild;
        }
    }
    cout << endl;
}

void Tree::iterativeInorder(Node *p) {
    stack<Node*> stk;
    while (p != nullptr || ! stk.empty()){
        if (p != nullptr){
            stk.emplace(p);
            p = p->lchild;
        } else {
            p = stk.top();
            stk.pop();
            cout << p->data << ", " << flush;
            p = p->rchild;
        }
    }
    cout << endl;
}

void Tree::iterativePostorder(Node *p) {
    stack<long int> stk;
    long int temp;
    while (p != nullptr || ! stk.empty()){
        if (p != nullptr){
            stk.emplace((long int)p);
            p = p->lchild;
        } else {
            temp = stk.top();
            stk.pop();
            if (temp > 0){
                stk.emplace(-temp);
                p = ((Node*)temp)->rchild;
            } else {
                cout << ((Node*)(-1 * temp))->data << ", " << flush;
                p = nullptr;
            }
        }
    }
    cout << endl;
}

int searchInorder(int inArray[], int inStart, int inEnd, int data){
    for (int i=inStart; i<=inEnd; i++){
        if (inArray[i] == data){
            return i;
        }
    }
    return -1;
}

Node* Tree::generateFromTraversal(int *inorder, int *preorder, int inStart, int inEnd) {
    // Reference: https://algorithms.tutorialhorizon.com/make-a-binary-tree-from-given-inorder-and-preorder-traveral/
    static int preIndex = 0;

    if (inStart > inEnd){
        return nullptr;
    }

    Node* node = new Node(preorder[preIndex++]);

    if (inStart == inEnd){
        return node;
    }

    int splitIndex = searchInorder(inorder, inStart, inEnd, node->data);
    node->lchild = generateFromTraversal(inorder, preorder, inStart, splitIndex-1);
    node->rchild = generateFromTraversal(inorder, preorder, splitIndex+1, inEnd);

    return node;
}


int main() {

    Tree bt;

    int preorder[] = {4, 7, 9, 6, 3, 2, 5, 8, 1};
    int inorder[] = {7, 6, 9, 3, 4, 5, 8, 2, 1};


    Node* T = bt.generateFromTraversal(inorder, preorder, 0, sizeof(inorder)/sizeof(inorder[0])-1);
    bt.Preorder(T);
    cout<<endl;

    cout << "Heigh :" << bt.Height(T)<<endl;
    cout << "Count :" << bt.Count(T)<<endl;
    cout << "Sum: " << bt.sum(T) << endl;
    cout << "# of degree 2 nodes: " << bt.deg2NodeCount(T) << endl;
    cout << "# of leaf nodes: " << bt.leafNodeCount(T) << endl;
    cout << "# of degree 1 or degree 2 nodes: " << bt.deg1ordeg2NodeCount(T) << endl;
    cout << "# of degree 1 nodes: " << bt.deg1NodeCount(T) << endl;

     bt.DestroyTree(T);

    return 0;
}

Quiz

Comment  Read more

24. Trees 2(Code)

19 Jun 2020 | Algorithm

Tree Traversals

Create Binary Search

Using STL Queue

#include <iostream>
#include <queue>

using namespace std;
class Node
{
public:
    int data;
    Node* lchild;
    Node* rchild;
};
class Tree
{
public:
    Tree(){root = nullptr;}
    void CreateTree();
    void Preorder()
    {
        Preorder(root);
    }
    void Preorder(Node* p);
    void Inorder(){ Inorder(root); }
    void Inorder(Node* p);
    void Postorder(){ Postorder(root); }
    void Postorder(Node* p);
    void Levelorder(){ Levelorder(root);}
    void Levelorder(Node* p);
    int Height(){ return Height(root);}
    int Height(Node* p);


private:
    int l = 0;
    int r = 0;
    Node* root;
};
int Tree::Height(Node* p)
{
    if(p==nullptr)
        return 0;

    l = Height(p->lchild);
    r = Height(p->rchild);

    if(l>r)
    {
        return l+1;
    }
    else
    {
        return r+1;
    }

}
void Tree::Levelorder(Node* p)
{
    queue<Node*> q;
    cout << root->data << " , ";
    q.push(root);
    Node* t = p;

    while(!q.empty())
    {
        t = q.front();
        q.pop();

        if(t->lchild)
        {
            cout<< t->lchild->data<<",";
            q.push(t->lchild);
        }
        if(t->rchild)
        {
            cout<<t->rchild->data<<",";
            q.push(t->rchild);
        }

    }
}
void Tree::Postorder(Node* p)
{
    if(p)
    {
        Inorder(p->lchild);
        Inorder(p->rchild);
        cout<<p->data;
    }
}
void Tree::Inorder(Node* p)
{
    if(p)
    {
        Inorder(p->lchild);
        cout<<p->data;
        Inorder(p->rchild);
    }
}
void Tree::Preorder(Node* p)
{
    if(p)
    {
        cout<<p->data<<" ";
        Preorder(p->lchild);
        Preorder(p->rchild);
    }
}
void Tree::CreateTree()
{
    Node* p;
    Node* t;
    int x;
    queue<Node*> q;

    cout<<"Enter Root value: ";
    cin>>x;
    cout<<endl;

    root = new Node;
    root->data =x;
    root->lchild = root->rchild = nullptr;
    q.push(root);
    while(!q.empty())
    {
        p=q.front();
        q.pop();
        cout<<"enter left child of " <<p->data << ": ";
        cin>>x;
        cout<<endl;
        if(x!=-1)
        {
            t = new Node;
            t->data = x;
            t->lchild = t->rchild = nullptr;
            p->lchild = t;
            q.push(t);
        }
        cout<<"enter Right child of " <<p->data << ": ";
        cin>>x;
        cout<<endl;
        if(x!=-1)
        {
            t = new Node;
            t->data = x;
            t->lchild = t->rchild = nullptr;
            p->rchild = t;
            q.push(t);
        }
    }
}
int main()
{
    Tree t;
    t.CreateTree();
    cout<<"Preorder";
    t.Preorder();
    cout<<endl;
    cout<<"Inorder ";
    t.Inorder();
    cout<<endl;
    cout<<"Postorder: ";
    cout<<endl;
    t.Postorder();
    cout<<"Levelorder: ";
    cout<<endl;
    t.Levelorder();
    cout<<"Height: ";
    cout<<endl;
    t.Height();

    return 0;
}

Iterative Traversals

#include <iostream>
#include <queue>
#include <stack>
using namespace std;
class Node
{
public:
    int data;
    Node* lchild;
    Node* rchild;
};
class Tree
{
public:
    Tree(){root = nullptr;}
    void CreateTree();
    void Preorder()
    {
        Preorder(root);
    }
    void Preorder(Node* p);
    void Inorder(){ Inorder(root); }
    void Inorder(Node* p);
    void Postorder(){ Postorder(root); }
    void Postorder(Node* p);
    void Levelorder(){ Levelorder(root);}
    void Levelorder(Node* p);
    int Height(){ return Height(root);}
    int Height(Node* p);
    void iterativePreorder(){iterativePreorder(root);}
    void iterativePreorder(Node* p);
    void iterativeIneorder(){iterativeIneorder(root);}
    void iterativeIneorder(Node* p);
    void iterativePostorder(){iterativePostorder(root);}
    void iterativePostorder(Node* p);
private:
    int l = 0;
    int r = 0;
    Node* root;
};
void Tree::iterativePostorder(Node* p)
{
    stack<Node*> stk;
    while(p!=nullptr || !stk.empty())
    {
        if(p!=nullptr)
        {
            stk.push(p);
            p = p->lchild;
        }
        else
        {
            p = stk.top();
            stk.pop();
            cout<<p->data <<", ";
            iterativePostorder(p->rchild);
            }
        }
    cout <<endl;
}
void Tree::iterativeIneorder(Node* p)
{
    stack<Node*> stk;
    while(p!=nullptr || !stk.empty())
    {
        if(p!=nullptr)
        {
            stk.push(p);
            p = p->lchild;
        }
        else
        {
            p = stk.top();
            stk.pop();
            cout << p->data << " , ";
            p = p->rchild;
        }
    }
    cout <<endl;

}
void Tree::iterativePreorder(Node* p)
{
    stack<Node*> stk;
    while(p!=nullptr || !stk.empty())
    {
        if(p!=nullptr)
        {
            cout << p->data << " , ";
            stk.push(p);
            p = p->lchild;
        }
        else
        {
            p = stk.top();
            stk.pop();
            p = p->rchild;
        }
    }
    cout <<endl;

}
int Tree::Height(Node* p)
{
    if(p==nullptr)
        return 0;

    l = Height(p->lchild);
    r = Height(p->rchild);

    if(l>r)
    {
        return l+1;
    }
    else
    {
        return r+1;
    }

}
void Tree::Levelorder(Node* p)
{
    queue<Node*> q;
    cout << root->data << " , ";
    q.push(root);
    Node* t = p;

    while(!q.empty())
    {
        t = q.front();
        q.pop();

        if(t->lchild)
        {
            cout<< t->lchild->data<<",";
            q.push(t->lchild);
        }
        if(t->rchild)
        {
            cout<<t->rchild->data<<",";
            q.push(t->rchild);
        }

    }
}
void Tree::Postorder(Node* p)
{
    if(p)
    {
        Inorder(p->lchild);
        Inorder(p->rchild);
        cout<<p->data;
    }
}
void Tree::Inorder(Node* p)
{
    if(p)
    {
        Inorder(p->lchild);
        cout<<p->data;
        Inorder(p->rchild);
    }
}
void Tree::Preorder(Node* p)
{
    if(p)
    {
        cout<<p->data<<" ";
        Preorder(p->lchild);
        Preorder(p->rchild);
    }
}
void Tree::CreateTree()
{
    Node* p;
    Node* t;
    int x;
    queue<Node*> q;

    cout<<"Enter Root value: ";
    cin>>x;
    cout<<endl;

    root = new Node;
    root->data =x;
    root->lchild = root->rchild = nullptr;
    q.push(root);
    while(!q.empty())
    {
        p=q.front();
        q.pop();
        cout<<"enter left child of " <<p->data << ": ";
        cin>>x;
        cout<<endl;
        if(x!=-1)
        {
            t = new Node;
            t->data = x;
            t->lchild = t->rchild = nullptr;
            p->lchild = t;
            q.push(t);
        }
        cout<<"enter Right child of " <<p->data << ": ";
        cin>>x;
        cout<<endl;
        if(x!=-1)
        {
            t = new Node;
            t->data = x;
            t->lchild = t->rchild = nullptr;
            p->rchild = t;
            q.push(t);
        }
    }
}
int main()
{
    Tree t;
    t.CreateTree();
    cout<<"Preorder";
    t.Preorder();
    cout<<endl;
    cout<<"Inorder ";
    t.Inorder();
    cout<<endl;
    cout<<"Postorder: ";
    cout<<endl;
    t.Postorder();
    cout<<"Levelorder: ";
    cout<<endl;
    t.Levelorder();
    cout<<"Height: ";
    cout<<endl;
    t.Height();

    cout<<"Iterative Preorder: ";
    cout<<endl;
    t.iterativePreorder();

    cout<<"Iterative inorder: ";
    cout<<endl;
    t.iterativeIneorder();

    cout<<"Iterative Postorder: ";
    cout<<endl;
    t.iterativePostorder();

    return 0;
}

Comment  Read more

23. Trees

19 Jun 2020 | Algorithm

Binary Tree

Number of Binary Tree

  1. Unlabelled Nodes
  2. Labelled Nodes

Height vs Nodes

Strict Binary Tree

  1. Strict / Proper/ Complete
  2. Height vs Nodes
  3. internal vs External Node.

  • e = i+1

M-ary Trees

Representation of Binary Tree

  1. Array Representation
  2. Linked Representation

Strick(complete) vs Complete(Almost complete)

Tree Traversals

Comment  Read more