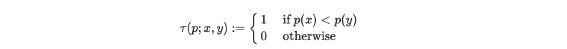11. Visual odometer(Feature point)

18 Jun 2020 | Visual SLAM

Feature Point

Basic concepts

Definition: The point of local uniqueness in the frame

It should be able to discern even if the object’s size, position, camera point of view, lighting, etc. change.

Applicable fields: recognition, detection, tracking, classification…

property

Repeatability: The same area can be found in different frame.

Differentiation: Feature points in different region have different expressions.

Efficiency: The number of feature points in the image should be smaller than the number of pixels.

Locality: Feature points relate only to the local area of the image.

Configuration(구성)

Keypoint: Location information of feature points

Descriptor: A vector describing information about surrounding pixels

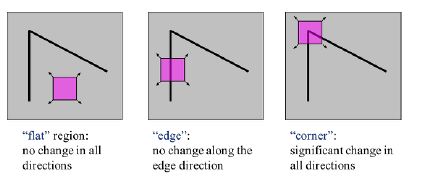
Harris corner detector

In a small window in an image, the part with large image change in all directions is regarded as a corner

The point where the image change value of the pixel is locally maximized is used as the corner point.

Shi-Tomasi

Good features should be able to be optimized for tracking algorithms!

Both simple translation and affine changes are considered.

Only the smallest of the two eigenvalues is considered.

Scale Invariant Feature Transform(SIFT)

You need strong points such as changes in size, direction and lighting!

Result of picking feature vectors for local patches centering on identifiable feature points

It expresses the direction and rapid degree of regional brightness change.

Due to the large amount of computation, it is not suitable for real-time SLAM implementation.

Of course, it can be complemented by GPU programming

The Difference of Gaussian method was used to compensate for the large amount of computation in the Laplacian of Gaussian method.

Laplacian: 2nd derivative of the brightness of the image

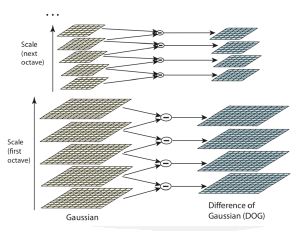
Difference of Gaussian(DoG)

Process

Scale-space extrema detection: Potential feature point candidates robust to changes in size and direction are extracted based on the difference of Gaussian for all scales.

keypoint localization: For each extrema, low-contrast points and points in the edge region are removed.

Orientation assignment: directional assignment based on local gradient for each point

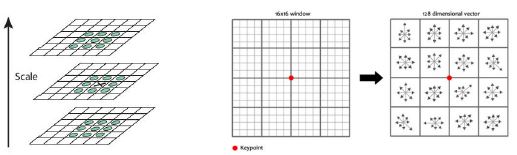
Keypoint descriptor: 16x16 size block -> 4x4 sub-block unit

Generate 8 bin histogram of direction in each sub-block

Finally, create a 128 dimensional vector

Oriented-FAST and Rotated-BRIEF(ORB)

quickly detect feature points based on the apparent change in brightness of grayscale

Binary Robust Independent Elementary Features(BRIEF)

Descriptor vector is composed of binary numbers.

Decide the binary number to treat as the vector through comparison between two pixels in the patch

Random two pixel pairs are randomly determined based on probability distribution

Generate 128bit binary descriptor by comparing 128 pairs

Oriented-FAST

The weakness of FAST is that it does not have direction and scale.

Solve scale immutability problems with image pyramids

Connect the geometric center O and the moment-based center C to find the direction for it

Rotated-BRIEF

Conventional BRIEF does not have rotational invariance

Use of keypoint direction information obtained during FAST detection

Use Steer BRIEF: Performs BRIEF after rotating according to the direction information

Correspondence matching(대응 매칭)

Basic concepts

Process required to perform data association process in SLAM

The process of correctly matching descriptors between images and images, or images and maps

Problems caused by repetitive textures can cause inconsistent accumulation!

Brute-force matcher

The point with the shortest descriptor distance between feature points in two different images is regarded as a matching point.

Generally, descriptor distance means similarity

Euclid distance, Hamming distance…

If the number of dots increases, the calculation amount increases, which is not efficient.

Fast Library for Approximate Nearest Neighbors(FLANN)

Matching library for fast matching in high Dimension

Real-time matching is suitable for SLAM

Reference

SLAM KR

Comment Read more

21. Stack

17 Jun 2020 | Algorithm

Stack using Array

#include <iostream>
using namespace std;
class Stack
{
private:
    int size_;
    int top;
    int* S;
public:
    Stack(int size_);
    ~Stack();
    void push(int x);
    int isFull();
    void display();
    int peek(int index);
    int stackTop();
    int isEmpty();
    int pop();
};
int Stack::pop()
{
    int x = 1;
    if(isEmpty())
    {
        cout<<"Stack UnderFLow"<<endl;
    }
    else
    {
        x = S[top];
        top--;
    }
    return x;
}
int Stack::isEmpty()
{
    if(top==-1)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}
int Stack::stackTop()
{
    if(isEmpty())
    {
        return -1;
    }
    return S[top];
}
int Stack::peek(int index)
{
    int x= -1;
    if(top-index+1<0 || top-index+1 == size_)
    {
        cout<<"invalid position"<<endl;
    }
    else
    {
        x = S[top-index+1];
    }
    return x;
}
void Stack::display()
{
    for(int i = top; i>=0; i--)
    {
        cout<<S[i]<<"|" << flush;
    }
    cout<< endl;
}
Stack::Stack(int size_)
{
    this->size_ = size_;
    top = -1;
    S = new int[size_];
}
Stack::~Stack()
{
    delete[] S;
}
void Stack::push(int x)
{
    if(isFull())
    {
        cout << "Stack OverFlow" <<endl;
    }
    else
    {
        top++;
        S[top]=x;
    }
}
int Stack::isFull()
{
    if(top==size_-1)
    {
        return 1;
    }
    return 0;
}
int main()
{
    int A[] = {1, 3, 5, 7, 9};
    Stack stk(sizeof(A)/sizeof(A[0]));
    // Populate stack with array elements
    for (int i=0; i<sizeof(A)/sizeof(A[0]); i++)
    {
        stk.push(A[i]);
    }
    stk.push(11);
    cout << "Stack full: " << stk.isFull() << endl;

    // Display stack;
    cout << "Stack: " << flush;
    stk.display();


    // Peek
    cout << "Peek at 0th: " << stk.peek(0) << endl;
    cout << "Peek at 3th: " << stk.peek(3) << endl;
    cout << "Peek at 10th: " << stk.peek(10) << endl;

    // Top element
    cout << "Top element: " << stk.stackTop() << endl;

    // Pop out elements from stack
    cout << "Popped out elements: " << flush;
    for (int i=0; i<sizeof(A)/sizeof(A[0]); i++)
    {
        cout << stk.pop() << ", " << flush;
    }

     cout << endl;
     stk.pop();
     cout<<"Stack empty: " << stk.isEmpty() << endl;
     return 0;
}

Stack using Linked List

#include <iostream>
using namespace std;
class Node
{
public:
    int data;
    Node* next;
};
class Stack
{
private:
    Node* top;
public:
    Stack();
    ~Stack();
    void push(int x);
    int peek(int index);
    int isEmpty();
    int stackTop();
    int isFull();
    int pop();
};
int Stack::pop()
{
    Node* p;
    int x = -1;
    if(top==nullptr)
    {
        cout << "Stack Underflow!" << endl;
    }
    else
    {
        p = top;
        x = p->data;
        top = top->next;
        delete p;
    }
    return x;
}
int Stack::isEmpty()
{
    if(top==nullptr)
        return 1;
    return 0;
}
Stack::peek(int index)
{
    if(isEmpty())
    {
        return -1;
    }
    else
    {
        Node* p =top;
        for(int i = 0; p!=nullptr&&i<index-1; i++)
        {
            p = p->next;
        }
        if (p!=nullptr)
        {
            return p->data;
        }
        else
        {
            return -1;
        }

    }
}
Stack::Stack()
{
    top = nullptr;
}
Stack::~Stack()
{
    Node* p = top;
    while(top)
    {
        top = top->next;
        delete p;
        p = top;
    }
}
void Stack::push(int x)
{
    Node* t = new Node;
    if(t==nullptr)
    {
        cout<<"Stack Overflow"<<endl;
    }
    else
    {
        t->data = x;
        t->next = top;
        top = t;
    }
}
int Stack::stackTop()
{
    if(top)
    {
        return top->data;
    }
    return -1;
}
int Stack::isFull()
{
    Node* t = new Node;
    int r=t?1:0;
    delete t;
    return r;
}
int main()
{
    int A[] = {1, 3, 5, 7, 9};
    Stack stk;
    // Populate stack with array elements
    for (int i=0; i<sizeof(A)/sizeof(A[0]); i++)
    {
        stk.push(A[i]);
    }
    cout << "Stack peek at 3rd: " << stk.peek(3) << endl;
    cout << "Stack peek at 10th: " << stk.peek(10) << endl;
    cout << "Stack top: " << stk.stackTop() << endl;
    cout << "Stack full: " << stk.isFull() << endl;
    cout << "Stack empty: " << stk.isEmpty() << endl;

    // Pop out elements from stack
    cout << "Popped: " << flush;
    for (int i=0; i<sizeof(A)/sizeof(A[0]); i++)
    {
        cout << stk.pop() << ", " << flush;
    }
    cout << endl;

    // Underflow
    cout << stk.pop() << endl;


    return 0;
}

Parenthesis Matching

#include <iostream>
#include <cstring>
using namespace std;
class Stack
{
private:
    int size_;
    int top_;
    char* S_;
public:
    Stack(int size_);
    ~Stack();
    int isEmpthy();
    int isFull();
    void push(char x);
    void pop();
};
void Stack::pop()
{
    if(isEmpthy())
    {
        cout<<"Stack underflow!"<<endl;
    }
    else
    {
        top_;;
    }
}
int Stack::isFull()
{
    if(top_==size_-1)
    {
      return 1;
    }

    return 0;
}
void Stack::push(char x)
{
    if(isFull())
    {
        cout<<"Stack OverFlow"<<endl;
    }
    else
    {
        top_++;
        S_[top_] = x;
    }

}

int Stack::isEmpthy()
{
    return (top_==-1)?1:0;
}
Stack::Stack(int size_)
{
    this->size_ = size_;
    top_ = -1;
    S_ = new char[size_];
}
Stack::~Stack()
{
    delete[] S_;
}
bool isBalance(char* exp)
{
    //create a stack
    Stack stk((int)strlen(exp)); // strlen is function that from cstring library
    // Process expression
    for(int i =0; i<strlen(exp);i++)
    {
        // found : pusth to stack
        if(exp[i]=='(')
        {
            stk.push(exp[i]);
        }
        else if(exp[i]==')')
        {
            // if stack is empthy : unbalanced expression
            if(stk.isEmpthy())
            {
                return false;
            }
            else
            {
                stk.pop();
            }
        }

    }
    return stk.isEmpthy()?true:false;

}
int main()
{
    char E[] = "((a+b)* (c-d))";
    cout<< isBalance(E)<<endl;

    return 0;
}

Extended Parenthesis Matching

#include <iostream>
#include <cstring>
#include <map>
using namespace std;
class Stack
{
private:
    int size_;
    int top_;
    char* S_;
public:
    Stack(int size_);
    ~Stack();
    int isEmpthy();
    int isFull();
    void push(char x);
    void pop();
    char top();
};
char Stack::top()
{
    return S_[top_];
}
void Stack::pop()
{
    if(isEmpthy())
    {
        cout<<"Stack underflow!"<<endl;
    }
    else
    {
        top_;;
    }
}
int Stack::isFull()
{
    if(top_==size_-1)
        return 1;
    return 0;
}
void Stack::push(char x)
{
    if(isFull())
    {
        cout<<"Stack OverFlow"<<endl;
    }
    else
    {
        top_++;
        S_[top_] = x;
    }

}

int Stack::isEmpthy()
{
    return (top_==-1)?1:0;
}
Stack::Stack(int size_)
{
    this->size_ = size_;
    top_ = -1;
    S_ = new char[size_];
}
Stack::~Stack()
{
    delete[] S_;
}
bool isBalance(char* exp)
{
    //Create a Map
    map<char, char> mapping;
    mapping['}'] = '{';
    mapping[')'] = '(';
    mapping[']'] = '[';

    // Create map iterator
    map<char, char>::iterator itr;

    //Create a Stack
    Stack stk((int)strlen(exp));

    for(int i =0;i<(int)strlen(exp);i++)
    {
        if(exp[i]==' { ' || exp[i]==' ( ' || exp[i]== ' [ ')
        {
            stk.push(exp[i]);
        }
        else
        {
            char temp = stk.top();
            if(temp == itr->second)// itr->first is key, itr->second is value
            {
                stk.pop();
            }
            else
            {
                return false;
            }
        }
    }
    return stk.isEmpthy()?true:false;
}
int main()
{
    char E[] = "{([a+b]* [c-d])/e}";
    cout<< isBalance(E)<<endl;

    return 0;
}

Comment Read more

20. Spares Matrix and Polynomial Using Linked list

17 Jun 2020 | Algorithm

Sparse Matrix Representation

Polynomial

struct Node
{
  int coeff;
  int exp;
  struct Node* next;
}*poly=NULL;

void create()
{
  struct Node* t;
  struct Node* last = NULL;
  int num, i;
  printf("Enter number of terms");
  scanf("%d",&num);
  printf("Enter each term with coeff and exp\n");
  for(i=0;i<num;i++)
  {
    t=(struct Node * )malloc(sizeof(struct Node));
    scanf("%d%d",&t->coeff,&t->exp);
    t->next=NULL;
    if(poly==NULL)
    {
      poly=last=t;
    }
    else
    {
      last->next=t;
      last=t;
    }
  }
}
void Display(struct Node *p)
{
  while(p)
  {
    printf("%dx%d +",p->coeff,p->exp);
    p=p->next;
  }
  printf("\n");
}
long Eval(struct Node *p, int x)
{
  long val=0;
  while(p)
  {
    val+=p->coeff*pow(x,p->exp);
    p=p->next;
  }
  return val;
}
int main()
{
  create();
  Display(poly);
  printf("%ld\n",Eval(poly,1));
  return 0;
}

Comment Read more

19. Linked List 4

17 Jun 2020 | Algorithm

C++ Class for Linked list

class Node
{
public:
  int data;
  Node* next;
};
class LinkedList
{
private:
  Node* first;
public:
  LinkedList(){first=NULL;}
  LinkedList(int A[], int n);
  ~LinkedList();
  void Display();
  void Insert(int index, int x);
  int Length();
  int Delete(int index);

};
LinkedList::LinkedList(int A[],int n)
{
  Node* last, * t;
  int i=0;

  first = new Node;
  first->data = A[0];
  first->next = NULL;
  last = first;
  for(i=1;i<n;i++)
  {
    t = new Node;
    t->data = A[i];
    t->next = NULL;
    last->next =t;
    last = t;
  }
}
LinkedList::~LinkedList()
{
  Node* p =first;
  while(first)
  {
    first = first->next;
    delete p;
    p = first;
  }
}
void LinkedList::Display()
{
  Node * p = first;
  while(p)
  {
    cout<<p->data<<" ";
    p=p->next;
  }
  cout<<endl;
}
void LinkedList::Insert(int index, int x)
{
  Node* t;
  Node* p = first;
  if(index<0||index> Length())
    return;
  t = new Node;
  t->data = x;
  t->next = NULL;
  if(index=0)
  {
    t->next = first;
    first = t;
  }
  else
  {
    for(int i=0; i<index-1;i++)
      p=p->next;
    t->next = p->next
    p->next = t;
  }
}
int LinkedList::Length()
{
  Node* p = first;
  int len=0;
  while(p)
  {
    len++
    p=p->next;
  }
  return len;
}
int LinkedList::Delete(int index)
{
  Node* p;
  Node* q = NULL;
  int x=-1;
  if (index<1 || index>Length())
    return -1;
  if(index==1)
  {
    p=first;
    first=first->next;
    x=p->data;
    delete p ;
  }
  else
  {
    p=first;
    for(int i=0; i<index-1; i++)
    {
      q=p;
      p=p->next;
    }
    q->next = p->next;
    x=p->data;
    delete p;
  }
  return x;
}
int main()
{
  int A[]={1,2,3,4,5};
  LinkedList l(A,5);

  l.Insert(3,10);
  l.Display();

  return 0;
}

Circular Linked list

class Node
{
public:
  int data;
  Node* next;
};
class CircularLinkedList
{
private:
  Node* head;
public:
  CircularLinkedList(int[] A, int n);
  ~CircularLinkedList();
  void Display();
  Node* getHead()
  {
    return head;
  }
  void recursiveDisplay(Node* p);
};
CircularLinkedList::CircularLinkedList(int[] A, int n)
{
  Node* t;
  Node* tail;

  head = new Node;

  head->data = A[0];
  head->next = head;
  tail = head;
  for(int i=1; i<n; i++)
  {
    t = new Node;
    t->data = A[i];
    t->next = tail->next;
    tail->next = t;
    tail = t;
  }
}
CircularLinkedList::~CircularLinkedList()
{
  Node* p = head;
  while(p->next!=head)
  {p=p->next;}
  while(p!=head)
  {
    p->next = head->next;
    delete head;
    head = p->next;
  }
  if(p==head)
  {
    delete head;
    head = nullptr;
  }
}
void CircularLinkedList::Display()
{
  Node* p = head;
  do{
    cout<<p->data<<"->"<<flush;
    p=p->next;
  }while(p!=head);
  cout << endl;
}
void CircularLinkedList::recursiveDisplay(Node *p)
{
  static int flag = 0;
  if(p!=head || flag ==0)
  {
    flag = 1;
    cout<<p->data<<"->"<<flush;
    recursiveDisplay(p->next);
    // Recursive를 해도 계속 flag는 1로 남는다.
  }
  flag =0;
}
int main()
{
  int A[]={1,3,5,7,9};

  CircularLinkedList cl(A, sizeof(A)/sizeof(A[0]));

  cl.Display();
  Node* h = cl.getHead();
  cl.recursiveDisplay(h);
}

Inserting or Deleting in circular linked list

#include <iostream>
using namespace std;

class Node{
public:
    int data;
    Node* next;
};

class CircularLinkedList{
private:
    Node* head;
public:
    CircularLinkedList(int A[], int n);
    void Display();
    void recursiveDisplay(Node* p);
    Node* getHead(){ return head; }
    ~CircularLinkedList();
    void Inserting(int index, int key);
    int Length();
    void Delete(int index);


};

CircularLinkedList::CircularLinkedList(int *A, int n) {

    Node* t;
    Node* tail;

    head = new Node;

    head->data = A[0];
    head->next = head;
    tail = head;

    for (int i=1; i<n; i++){
        t = new Node;
        t->data = A[i];
        t->next = tail->next;
        tail->next = t;
        tail = t;
    }
}

void CircularLinkedList::Display() {
    Node* p = head;
    do {
        cout << p->data << " -> " << flush;
        p = p->next;
    } while (p != head);
    cout << endl;
}

void CircularLinkedList::recursiveDisplay(Node *p) {
    static int flag = 0;
    if (p != head || flag == 0){
        flag = 1;
        cout << p->data << " -> " << flush;
        recursiveDisplay(p->next);
    }
    flag = 0;
    cout << endl;
}
int CircularLinkedList::Length()
{
    Node* p = head;
    int len=0;
    do
    {
        len++;
        p=p->next;
    }while(p!=head);
    return len;
}
void CircularLinkedList::Inserting(int index, int key)
{
    Node* t;
    Node* p = head;
    int i;
    if(index<0 || index>Length())
        return;
    if(index ==0)
    {
        t = new Node;
        t->data = key;
        if(head==NULL)
        {
            head = t;
            head->next = head;
        }
        else
        {
            while(p->next!=head)
            {
                p = p->next;
            }
            p->next = t;
            t->next = head;
            head = t;

        }
    }
    else
    {
        for(i=0;i<index-1;i++)
        {
            p=p->next;
        }
        t = new Node;
        t->data = key;
        t->next = p->next;
        p->next = t;
    }

}
void CircularLinkedList::Delete(int index)
{
    Node* q;
    Node* p = head;
    int i,x;

    if(index<0 || index>Length())
        return;
    if(index==1)
    {
        while(p->next != head)
        {
            p=p->next;
        }
        x= head->data;
        if(head = p)
        {
            delete head;
            head =NULL;
        }
        else
        {
            p->next = head->next;
            delete head;
            head = p->next;
        }
    }
    else
    {
        for(i=0;i<index-2;i++)
        {
            p=p->next;
        }
        q = p->next;
        p->next = q->next;
        x=q->data;
        delete q;
    }

}
CircularLinkedList::~CircularLinkedList() {
    Node* p = head;
    while (p->next != head){
        p = p->next;
    }

    while (p != head){
        p->next = head->next;
        delete head;
        head = p->next;
    }

    if (p == head){
        delete head;
        head = nullptr;
    }

}


int main() {

    int A[] = {1, 3, 5, 7, 9};

    CircularLinkedList cl(A, sizeof(A)/sizeof(A[0]));

    cl.Display();

    cl.Inserting(3,6);
    Node* h = cl.getHead();
    cl.recursiveDisplay(h);

    cl.Delete(3);

    cl.Display();

    return 0;
}

Reserve for Doubly Linked list

#include <iostream>
using namespace std;

class Node
{
public:
  int data;
  Node* prev;
  Node* next;
};
class DoublyLinkedList
{
private:
  Node* head;
public:
    DoublyLinkedList();
    DoublyLinkedList(int A[], int n);
    ~DoublyLinkedList();
    int Length();
    void insert_(int index, int x);
    void Display();
    void Delete(int index);
    void Reverse();
};
void DoublyLinkedList::Delete(int index)
{
    Node* p = head;
    if(index<0 || index>Length())
    {
        return;
    }
    if(index ==1)
    {
        head = head->next;
        if(head)
        {
            head->prev =nullptr;
        }
        delete p;
    }
    else
    {
        for(int i=0; i<index-1; i++)
        {
            p=p->next;
        }
        p->prev->next = p->next;
        if(p->next)
        {
            p->next->prev = p->prev;
        }
        delete p;
    }


}
void DoublyLinkedList::Display()
{
    Node* p = head;
    while(p!=nullptr)
    {
        cout<<p->data<<flush;
        p=p->next;
        if(p!=nullptr)
            cout<<" <-> "<<flush;
    }
    cout<<endl;
}
DoublyLinkedList::Length()
{
    int length = 0;
    Node* p =head;
    while(p!=nullptr)
    {
        length++;
        p=p->next;
    }
    cout<<endl;
    return length;

}
DoublyLinkedList::DoublyLinkedList()
{
    head = new Node;
    head->prev = nullptr;
    head->next = nullptr;
}
DoublyLinkedList::DoublyLinkedList(int A[], int n)
{
    head = new Node;
    head->prev = nullptr;
    head->next = nullptr;
    head->data = A[0];
    Node* tail = head;
    for (int i=1; i<n; i++)
    {
        Node* t = new Node;
        t->prev = tail;
        t->data = A[i];
        t->next = tail->next; // tail->next is points to null
        tail->next = t;
        tail = t;
    }
}
void DoublyLinkedList::Reverse()
{
    Node* p = head;
    Node* temp;
    while(p!=nullptr)
    {
        temp = p->next;
        p->next = p->prev;
        p->prev = temp;
        p = p->prev;
        //Need to check the following condition again
        if(p->next == nullptr)
        {
            p->next = p->prev;
            p->prev = nullptr;
            head = p;
            break;
        }
    }
}
void DoublyLinkedList::insert_(int index, int x)
{
    if(index<0 || index> Length())
        return;

    Node* p=head;
    Node* t= new Node;
    t->data = x;
    if(index ==0)
    {
        t->prev = nullptr;
        t->next = head;
        head->prev = t;
        head = t; // pointing the "head" changed to t as new head pointer;
    }
    else
    {
        for(int i=0; i<index-1;i++)
        {
            p=p->next;
        }
        t->prev = p;
        t->next = p->next;
        if(p->next){
            p->next->prev = t;
        }
        p->next = t;
    }
}
DoublyLinkedList::~DoublyLinkedList()
{
    Node* p =head;
    while(head)
    {
        head = head->next;
        delete p;
        p = head;
    }
}
int main()
{
  int A[]={1,3,5,7,9};
  DoublyLinkedList dll(A, sizeof(A)/sizeof(A[0]));
  cout<<"length : "<<dll.Length();
  dll.insert_(0,11);
  dll.insert_(6,13);
  dll.Display();
  dll.Delete(6);
  dll.Delete(1);
  dll.Display();
  dll.Reverse();
  dll.Display();
  return 0;
}

Finding Middle Element of a Linked list

#include <iostream>
#include <cmath>
#include <stack>

using namespace std;
class Node
{
public:
    int data;
    Node* next;
};
Node* head = new Node;
void create(int A[], int n)
{
    Node* temp;
    Node* tail;
    head->data = A[0];
    head->next = nullptr;
    tail = head;
    for(int i=1; i<n;i++)
    {
        temp = new Node;
        temp->data = A[i];
        temp->next = nullptr;
        tail->next = temp;
        tail = temp;
    }
}
void middleNode1(Node* p)
{
    Node* t = p;
    int length =0;
    while(t)
    {
        length++;
        t=t->next;
    }
    int index = length/2;
    Node* q=head;
    for(int i =0; index-1; i++)
    {
        q = q->next;
    }
        cout << "Middle Element (Method-I): " << q->data << endl;
}
void middleNode2(Node* p){
    Node* q = p;
    while (q){
        q = q->next;
        if (q){
            q = q->next;
        }
        if (q){
            p = p->next;
        }
    }
    cout << "Middle Element (Method-II): " << p->data << endl;
}
void middleNode3(Node* p){
    stack<Node*> s;
    while (p){
        s.push(p);
        p = p->next;
    }
    int length = s.size();
    int popLength = (int)(floor(length/2.0));
    while (popLength){
        s.pop();
        popLength--;
    }
    cout << "Middle Element (Method-III): " << s.top()->data << endl;
}
int main()
{
    int A[]={1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21};
    create(A,sizeof(A)/sizeof(A[0]));
    cout << endl;

    middleNode1(head);

    return 0;
}

Finding Intersecting point of two linked list.

#include <iostream>
#include <cmath>
#include <stack>

using namespace std;
class Node
{
public:
    int data;
    Node* next;
};
Node* head = new Node;
void create(int A[], int n){
    Node* temp;
    Node* tail;

    head->data = A[0];
    head->next = nullptr;
    tail = head;

    for (int i=1; i<n; i++){
        temp = new Node;
        temp->data = A[i];
        temp->next = nullptr;
        tail->next = temp;
        tail = temp;
    }
}
Node* second = new Node;
void createSecond(int A[], int n, Node* p)
{
    Node* temp;
    Node* tail;
    second->data = A[0];
    second->next = nullptr;
    tail = second;
    for(int i=1; i<n;i++)
    {
        temp = new Node;
        temp->data = A[i];
        temp->next = nullptr;
        tail->next = temp;
        tail = temp;
    }
    tail->next = p;

}
void Intersection(Node* p, Node* q)
{
    //Populate first stack;
    stack<Node*> stk1;
    while(p!=nullptr)
    {
        stk1.push(p);
        p=p->next;
    }

    //Populate second stack
    stack<Node*> stk2;
    while(q!=nullptr)
    {
        stk1.push(q);
        q=q->next;
    }

    Node* r;
    while(stk1.top()==stk2.top())
    {
        r = stk1.top();
        stk1.pop();
        stk2.pop();
    }
    cout << "Intersecting Node: " << r->data << endl;
}
int main()
{
    // Create First Linked List
    int A[]={1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21};
    create(A,sizeof(A)/sizeof(A[0]));

    // Create Second Linked List
    Node* temp = head;
    int i = 5;
    while (i>0)
    {
        temp = temp->next;
        i--;
    }
    cout << temp->data << endl;

    int B[] = {2, 4, 6, 8, 10};
    createSecond(B, sizeof(B)/sizeof(B[0]), temp);

    //Find Intersection
    Intersection(head,second);

    return 0;
}