for Robot Artificial Inteligence

22. Queue

18 Jun 2020 | Algorithm

Queue using Array

#include <iostream>
using namespace std;
class Queue
{
private:
    int size_;
    int front_;
    int rear;
    int* Q;
public:
    Queue(int size_);
    ~Queue();
    void enqueue(int x);
    int isFull();
    void display();
    int isEmpty();
    void dequeue();
};
int Queue::isEmpty()
{
    if(front_==rear)
    {
        return 1;
    }
    return 0;
}
void Queue::dequeue()
{
    if(isEmpty())
    {
        cout<<"Queue Empty"<<endl;
    }
    else
    {
        front_++;
    }
}
void Queue::display()
{
    if(isEmpty())
    {
        cout<<"Queue is Empty"<<endl;
    }
    else
    {
        for(int i=0; i<size_;i++)
        {
            cout<<Q[i]<< " ";
        }
    }
    cout<<endl;
}
int Queue::isFull()
{
    if(rear==size_-1)
        return 1;
    return 0;
}
void Queue::enqueue(int x)
{
    if(isFull())
    {
        cout << "Queue Overflow" << endl;
    }
    else
    {
        rear++;
        Q[rear]=x;
    }
}
Queue::Queue(int size_)
{
    this->size_ = size_;
    front_ = -1;
    rear = -1;
    Q = new int[size_];
}
Queue::~Queue()
{
    delete[] Q;
}
int main()
{
    // Create Queue
    int A[] = {1, 3, 5, 7, 9};
    Queue q(sizeof(A)/sizeof(A[0]));

    //Enqueue
    for(int i =0; i<sizeof(A)/sizeof(A[0]);i++)
    {
        q.enqueue(A[i]);
    }

    // Display
    q.display();

    // Overflow
    q.enqueue(10);

    // Dequeue
    for(int i =0; i<sizeof(A)/sizeof(A[0]);i++)
    {
        q.dequeue();
    }

    // Underflow
    q.dequeue();

}

Queue using Linked List

#include <iostream>

using namespace std;

class Node{
public:
    int data;
    Node* next;
};

class Queue{
private:
    Node* front;
    Node* rear;
public:
    Queue();
    ~Queue();
    void enqueue(int x);
    int dequeue();
    bool isEmpty();
    void display();
};

Queue::Queue() {
    front = nullptr;
    rear = nullptr;
}

void Queue::enqueue(int x) {
    Node* t = new Node;
    if (t == nullptr){
        cout << "Queue Overflow" << endl;
    } else {
        t->data = x;
        t->next = nullptr;
        if (front == nullptr){
            front = t;
            rear = t;
        } else {
            rear->next = t;
            rear = t;
        }
    }
}

int Queue::dequeue() {
    int x = -1;
    Node* p;
    if (isEmpty()){
        cout << "Queue Underflow" << endl;
    } else {
        p = front;
        front = front->next;
        x = p->data;
        delete p;
    }
    return x;
}

bool Queue::isEmpty() {
    if (front == nullptr){
        return true;
    }
    return false;
}

Queue::~Queue() {
    Node* p = front;
    while (front){
        front = front->next;
        delete p;
        p = front;
    }
}

void Queue::display() {
    Node* p = front;
    while (p){
        cout << p->data << flush;
        p = p->next;
        if (p != nullptr){
            cout << " <- " << flush;
        }
    }
    cout << endl;
}

int main() {

    int A[] = {1, 3, 5, 7, 9};

    Queue q;

    for (int i=0; i<sizeof(A)/sizeof(A[0]); i++){
        q.enqueue(A[i]);
    }

    q.display();

    for (int i=0; i<sizeof(A)/sizeof(A[0]); i++){
        q.dequeue();
    }
    q.dequeue();

    return 0;
}

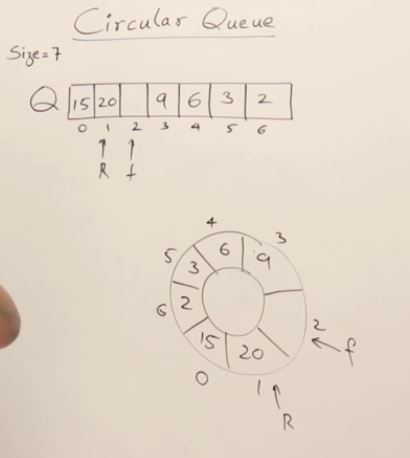
Circular Queue

#include <iostream>

using namespace std;

class CircularQueue
{
private:
    int size_;
    int rear_;
    int front_;
    int* Q;
public:
    CircularQueue(int size_);
    ~CircularQueue();
    void enqueue(int x);
    int isFull();
    void Display();
    int dequeue();
};
void CircularQueue::Display()
{
    int i = front_ +1;
    do{
        cout<<Q[i]<<flush;
        if(i<rear_)
        {
            cout<<" <- " << flush;
        }
        i = (i+1)%size_;
    }while(i!=(rear_+1)%size_);
}
int CircularQueue::isFull()
{
    if(rear_ == size_-1)
        return 1;
    return 0;
}
void CircularQueue::enqueue(int x)
{
    if(isFull())
    {
        cout<< "Queue Overflow" << endl;
    }
    else
    {
        rear_ = (rear_+1)%size_;
        Q[rear_] = x;
    }

}
int CircularQueue::dequeue()
{
    int x = -1;
    if(front_==rear_)
    {
        cout<<"Queue Underflow"<<endl;
    }
    else
    {
        front_ = (front_+1)%size_;
        x = Q[front_];
    }
    return x;

}
CircularQueue::CircularQueue(int size_)
{
    this->size_ = size_;
    rear_ =-1;
    front_ = -1;
    Q = new int[size_];
}
CircularQueue::~CircularQueue()
{
    delete[] Q;
}

int main()
{
    int A[] = {1, 3, 5, 7, 9};

    CircularQueue cq(sizeof(A)/sizeof(A[0]));

    // Enqueue
    for(int i =0; i<sizeof(A)/sizeof(A[0]); i++)
    {
        cq.enqueue(A[i]);
    }

    //Display
    cq.Display();
    cout<<endl;

    // Over Flow
    cq.enqueue(10);

    //Dequeue
    for(int i=0; i<sizeof(A)/sizeof(A[0]);i++)
    {
        cq.dequeue();
    }
    // Underflow
    cq.dequeue();
    return 0;
}

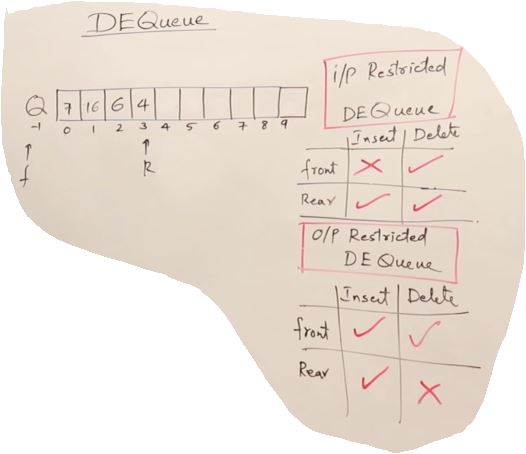
Double Ended Queue(DEQueue)

#include <iostream>

using namespace std;

class DEQueue{
private:
    int front;
    int rear;
    int size;
    int* Q;

public:
    DEQueue(int size);
    ~DEQueue();
    void display();
    void enqueueFront(int x);
    void enqueueRear(int x);
    int dequeueFront();
    int dequeueRear();
    bool isEmpty();
    bool isFull();
};

DEQueue::DEQueue(int size) {
    this->size = size;
    front = -1;
    rear = -1;
    Q = new int [size];
}

DEQueue::~DEQueue() {
    delete [] Q;
}

bool DEQueue::isEmpty() {
    if (front == rear){
        return true;
    }
    return false;
}

bool DEQueue::isFull() {
    if (rear == size - 1){
        return true;
    }
    return false;
}

void DEQueue::enqueueFront(int x) {
    if (front == -1){
        cout << "DEQueue Overflow" << endl;
    } else {
        Q[front] = x;
        front--;
    }
}

void DEQueue::enqueueRear(int x) {
    if (isFull()){
        cout << "DEQueue Overflow" << endl;
    } else {
        rear++;
        Q[rear] = x;
    }
}

int DEQueue::dequeueFront() {
    int x = -1;
    if (isEmpty()){
        cout << "DEQueue Underflow" << endl;
    } else {
        x = Q[front];
        front++;
    }
    return x;
}

int DEQueue::dequeueRear() {
    int x = -1;
    if (rear == -1){
        cout << "DEQueue Underflow" << endl;
    } else {
        x = Q[rear];
        rear--;
    }
    return x;
}

void DEQueue::display() {
    for (int i=front+1; i<=rear; i++) {
        cout << Q[i] << flush;
        if (i < rear){
            cout << " <- " << flush;
        }
    }
    cout << endl;
}

int main() {

    int A[] = {1, 3, 5, 7, 9};
    int B[] = {2, 4, 6, 8};

    DEQueue deq(sizeof(A)/sizeof(A[0]));

    for (int i=0; i<sizeof(A)/sizeof(A[0]); i++){
        deq.enqueueRear(A[i]);
    }
    deq.display();
    deq.enqueueRear(11);

    for (int i=0; i<sizeof(A)/sizeof(A[0]); i++){
        deq.dequeueFront();
    }
    deq.dequeueFront();

    cout << endl;

    for (int i=0; i<sizeof(B)/sizeof(B[0]); i++){
        deq.enqueueFront(B[i]);
    }
    deq.display();
    deq.enqueueFront(10);
    deq.enqueueFront(12);

    for (int i=0; i<sizeof(B)/sizeof(B[0]); i++){
        deq.dequeueRear();
    }
    deq.display();
    deq.dequeueRear();
    deq.dequeueRear();

    return 0;
}

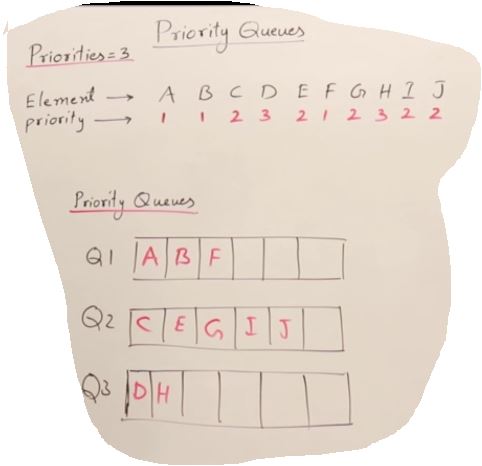
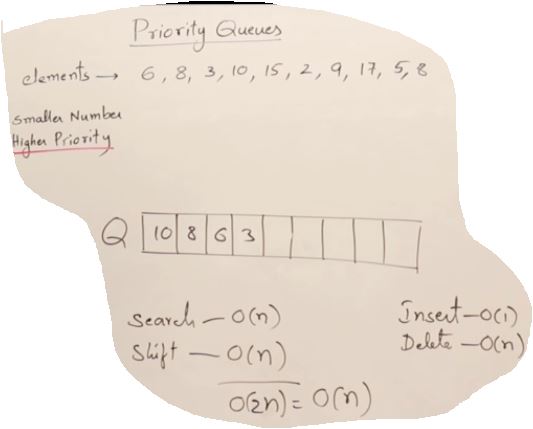
Priority Queue

  • Limited set of priority
  • Element Priority

Queue using 2 stacks

#include <iostream>
#include <stack>

using namespace std;
class Queue
{
private:
    stack<int> e_stk;
    stack<int> d_stk;
public:
    Queue(){};
    ~Queue(){};
    void enqueue(int x);
    int dequeue();
};
int Queue::dequeue()
{
    int x= -1;
    if (d_stk.empty())
    {
        if(e_stk.empty())
        {
            cout << "Queue Underflow" << endl;
            return x;
        }
        else
        {
            while (!e_stk.empty())
            {
                d_stk.push(e_stk.top());
                e_stk.pop();
            }

        }
    }
    x = d_stk.top();
    d_stk.pop();
    return x;
}
void Queue::enqueue(int x)
{
    e_stk.push(x);
}
int main()
{
    int A[] = {1,3,5,7,9};
    Queue q;

    cout<<"Enqueue"<<flush;
    for(int i =0; i<sizeof(A)/sizeof(A[0]);i++)
    {
        q.enqueue(A[i]);
        cout<<A[i]<<flush;
        if(i<sizeof(A)/sizeof(A[0])-1)
        {
            cout<< "<-"<<flush;
        }
    }
    cout << endl;

    cout<< "Dequeue"<<flush;
    for (int i=0; i<sizeof(A)/sizeof(A[0]); i++)
    {
        cout << q.dequeue() << flush;
        if (i < sizeof(A)/sizeof(A[0])-1){
                cout<<" <- " <<flush;
        }
    }

    return 0;

}

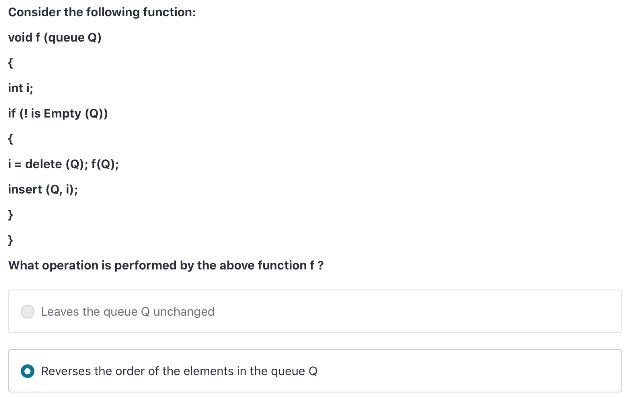
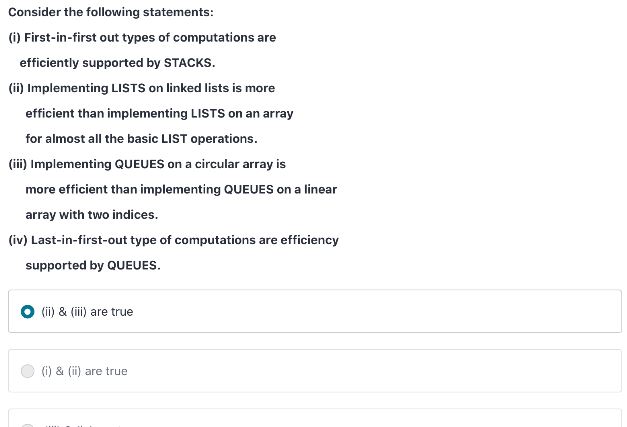
Quiz

Comment  Read more

21. Stack 2

18 Jun 2020 | Algorithm

Infix to postfix Conversion

struct Node
{
  char data;
  struct Node* next;
}*top=NULL;

void push(char x)
{
  struct Node* t;
  t = new Node;

  if(t=NULL)
  {
    printf("stack is full \n");
  }
  else
  {
    t->data = x;
    t->next = top;
    top = t;
  }
}
int isOperand(char x)
{
  if(x=='+' || x=='-' || x=='*' || x=='/')
  {
    return 0;
  }
  else
    return 1;

}
char* IntoPost (char* infix)
{
  int i=0, j=0;
  char* postfix;
  int len=strlen(infix);
  postfix = new char[len+2]
  while(infix[i]!='\0')
  {
    if(isOperand(infix[i]))
    {
      postfix[j++] = infix[i++];
    }
    else
    {
      if(pre(infix[i])>pre(top->data))
      {
        push(infix[i++]);
      }
      else
      {
        postfix[j++] = pop();
      }
    }
  }
  while(top!=NULL)
  {
    postfix[j++]=pop();
  }
  postfix[j] = '\0';
  return postfix;
}
char pop()
{
  struct Node* t;
  char x=1;
  if (top==NULL)
  {
    printf("Stack is Empthy")
  }
  else
  {
    t= top;
    top = top->next;
    x = t->data;
    free(t);
  }
  return x;
}
int pre(char x)
{
  if(x=='+' || x=='-')
    retrun 1;
  else if(x=='*' || x=='/')
    return 2;
  return 0;
}
int main()
{
  char* infix="a+b*c-d/e";
  push('#');
  char* postfix = InToPost(infix);
  printf("%s", postfix);
  return 0;
}

Infix to postfix with Associativity and parenthesis

  • Associativity
  • Unary(1진법) Operation


#include <iostream>
#include<cstring>
#include <stack>
using namespace std;

int isOperand(char x)
{
    if (x == '+' || x == '-' || x == '*' || x == '/' ||
        x == '^' || x == '(' || x == ')'){
        return 0;
    }
    return 1;
}
int outPrecedence(char x)
{
    if (x == '+' || x == '-'){
        return 2;
    } else if (x == '*' || x == '/'){
        return 4;
    } else if (x == '^'){
        return 5;
    } else if (x == '('){
        return 0;
    }
    return -1;
}
int inPrecedence(char x){
    if (x == '+' || x == '-'){
        return 2;
    } else if (x == '*' || x == '/'){
        return 4;
    } else if (x == '^'){
        return 5;
    } else if (x == '('){
        return 0;
    }
    return -1;
}
char* convert(char* infix)
{
    char* postfix = new char[strlen(infix)+1];

    stack<char> stk;

    int i = 0;
    int j = 0;

    while(infix[i]!='\0')
    {
        if(isOperand(infix[i]))
        {
            postfix[j++] = infix[i++];
        }
        else
        {
            if(stk.empty() || outPrecedence(infix[i])>inPrecedence(stk.top()))
            {
                stk.push(infix[i++]);
            }
            else if (outPrecedence(infix[i]) == inPrecedence(stk.top()))
            {
                stk.pop();
            }
            else
            {
                postfix[j++] = stk.top();
                stk.pop();
            }

        }
    }
    while(!stk.empty()&&stk.top()!=')')
    {
        postfix[j++] = stk.top();
        stk.pop();
    }
    postfix[j] = '\0';

    return postfix;
}


int main()
{
    char infix[] = "((a+b)* c)-d^e^f";
    cout << convert(infix) << endl;
    return 0;
}

Evaluation of Post fix

#include <iostream>
#include<cstring>
#include <stack>
using namespace std;
int isOperand(char x)
{
    if(x == '+' || x=='-'|| x=='*'|| x=='/')
    {
        return 0;
    }
    return 1;
}
int operation(char op, int x, int y)
{
    if (op == '+'){
        return x + y;
    } else if (op == '-'){
        return x - y;
    } else if (op == '*'){
        return x * y;
    } else if (op == '/'){
        return x / y;
    }
}
int Evaluate(char* postfix)
{
    stack<char> stk;
    int x, y, result;
    for(int i =0; postfix[i]!='\0';i++)
    {
        if(isOperand(postfix[i]))
        {
            // int typecast would not work because of char so subtract '0'
            stk.push(postfix[i]-'0');
        }
        else
        {
            y=stk.top();
            stk.pop();
            x=stk.top();
            stk.pop();
            result = operation(postfix[i], x,y);
            stk.push(result);
        }
    }
    result = stk.top();
    stk.pop();
    return result;
}

int main()
{
    char postfix[] = "35*62/+4-";
    cout << Evaluate(postfix) << endl;
    cout << postfixEvaluate(postfix) << endl
}

Quiz

Comment  Read more

14. Visual odometer(3D-3D Matching(3D-3D로 자세 추정 방법))

18 Jun 2020 | Visual SLAM

Recap

Introduction

  • 서로 대응 관계를 이미 알고 있을때 3D-3D 매칭은 쉽게 풀 수 있다.

선형 방법 -SVD

Reference

SLAM KR

Comment  Read more

13. Visual odometer(3D-2D Matching(3D-2D로 자세 추정 방법))

18 Jun 2020 | Visual SLAM

Recap

  • 2D-2D: epipolar geometry
    • Using a pair of feature points on a 2D image

Introduction

  • 3D-2D Matching : PnP(Perspective-n-Point)
    • estimate the camera’s pose movement given the correspondence between 3D and 2D
    • 3D: Camera coordinate system or world coordinate system
    • 2D: Image coordinate system
    • Used for RGB-D odometry, calibration, etc.
    • Motion estimation without epipolar constraints is possible even in environments where the number of matching points is small.
    • Method(linear, Non-linear):
      • DLT(Direct Linear Transformation)
      • P3P
      • EPnP(Efficient PnP)
      • UPnP
      • Bundle Adjustment

Direct Linear Transform, DLT

  • Linear change relational solution
    • Each feature point provides two linear equations for t
    • T has a total of 12 dimensions, so at least 6 pairs are required. (Actually 11, 5.5 pairs)
    • Find the least squares solution for the over-determined equation using the method as SVD.
    • Find the optimum value of R and t using methods such as QR decomposition
    • Here, it is assumed that it is calibrated, so internal parameters are not considered.

P3P

  • Solve problems using only 3 pairs of match points.
  • Using a triangular match (shares the angle of incidence for the camera optical center O).
  • The location of A, B, and C in the world coordinate system, not the camera coordinate system.

Bundle Adjustment

  • Bundle: A bundle of multiple light rays
  • solve the nonlinear least squares problem
    • Linear Method: Often find the camera posture first, then the location of the space(Cloused-form solution)
    • Nonlinear method: Optimize the camera posture and spatial point position together by considering them as optimization variables. (Non-linear optimization, iterative solution)
  • Bundle adjustment in PnP minimizes reprojection errors.
  • R, t calculation using Lie algebra

Reference

SLAM KR

Comment  Read more

12. Visual odometer(2D-2D Matching & Triangulation(2D로 자세 추정 방법))

18 Jun 2020 | Visual SLAM

Epipolar Geometry - Epipolar constraint

Epipolar Geometry - Essential Matrix

Triangulation

Homograph

Reference

SLAM KR

Comment  Read more