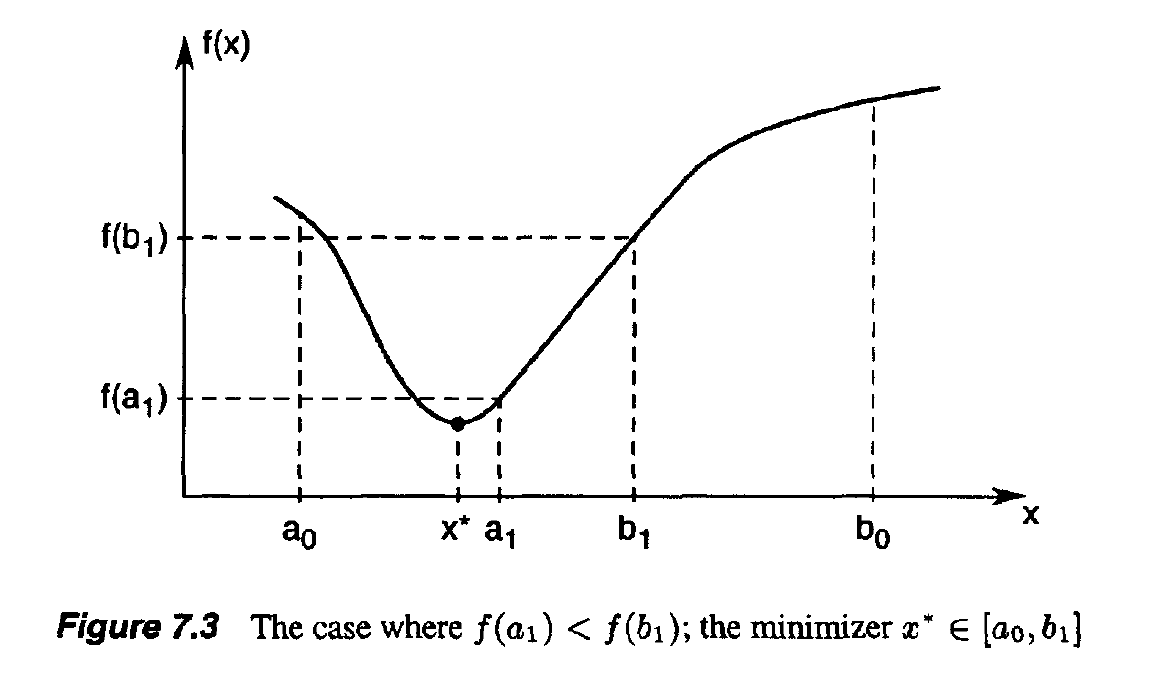
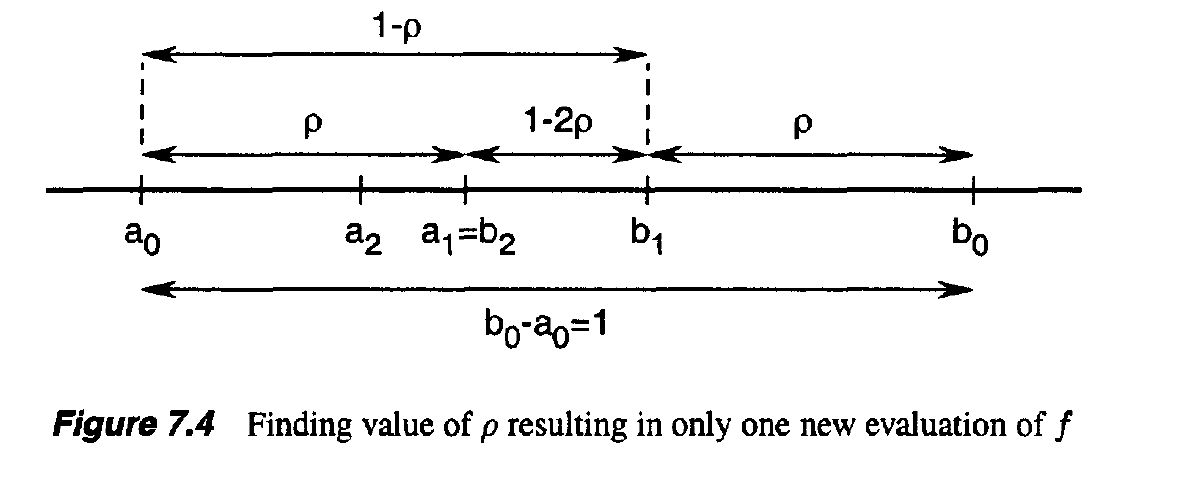
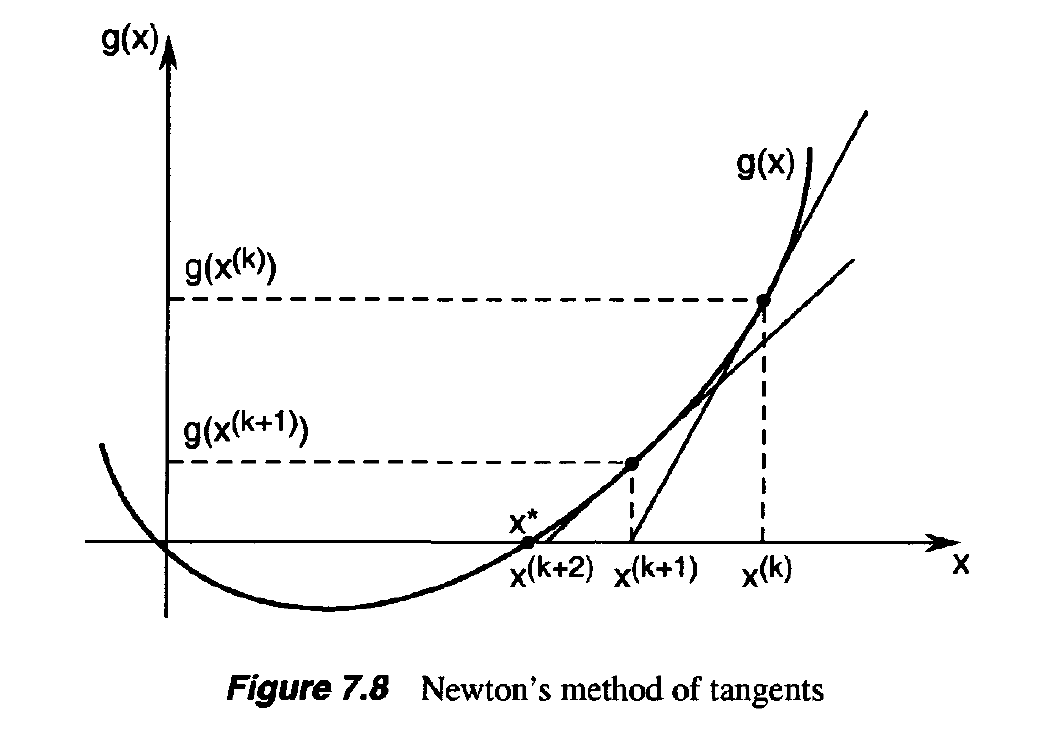
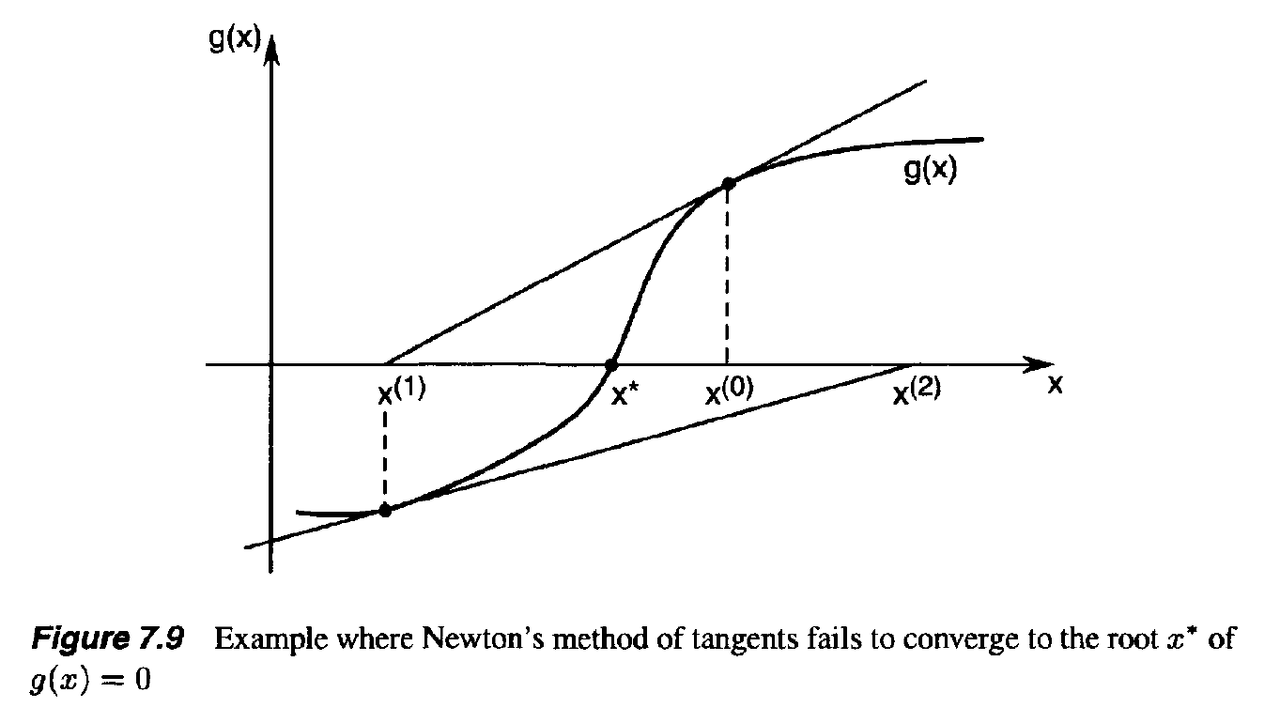
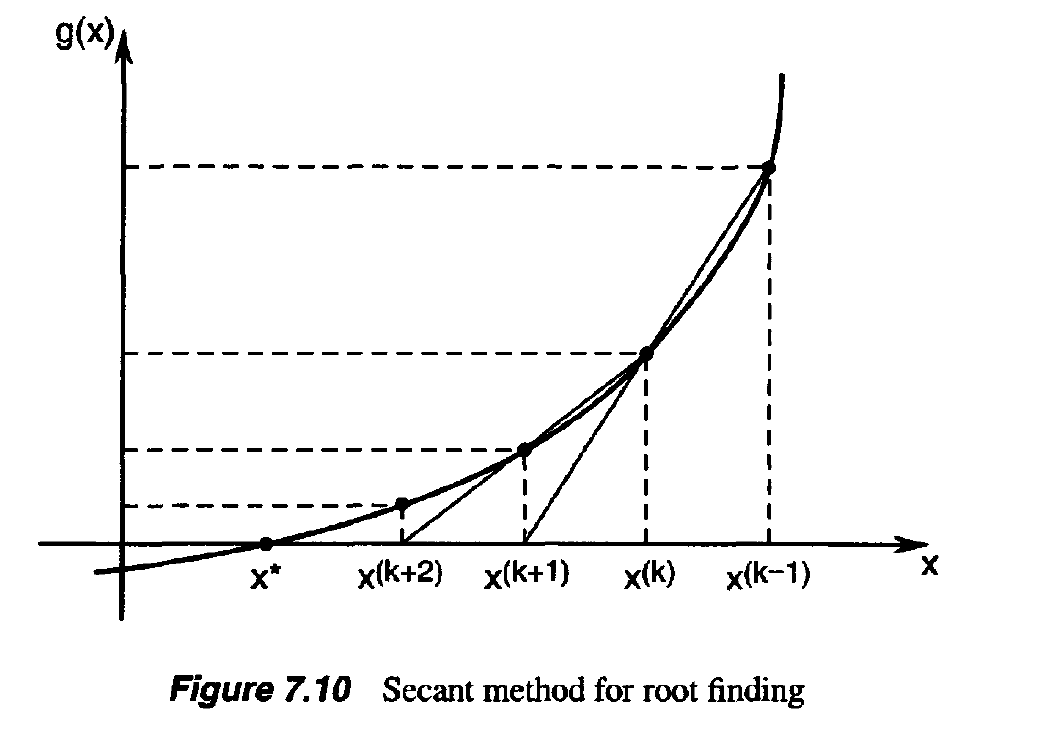
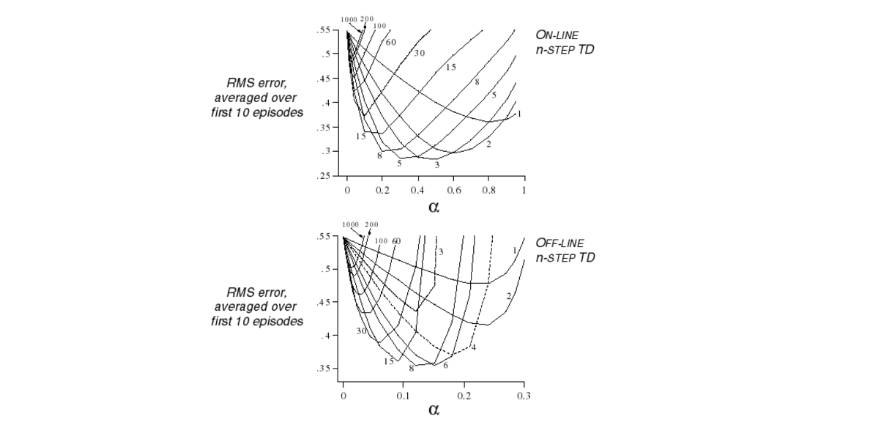
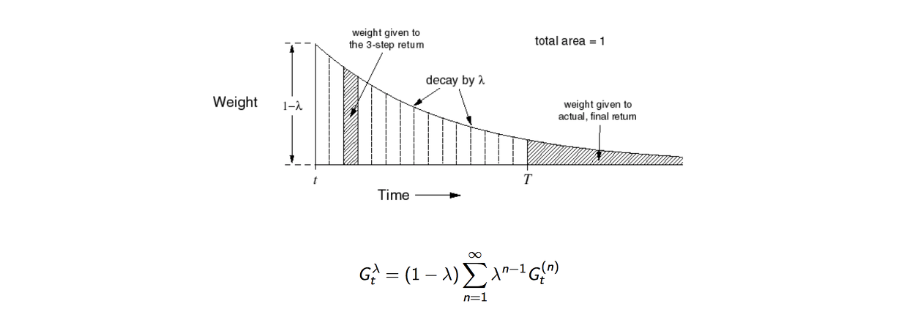
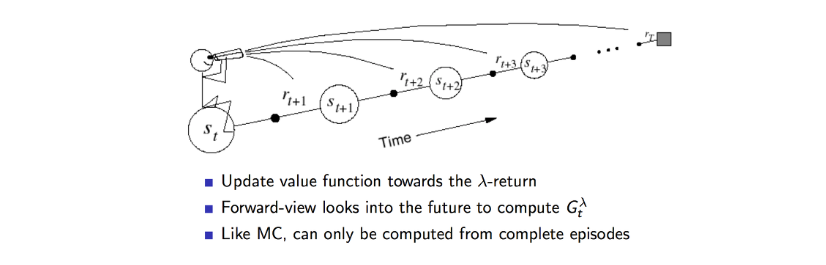
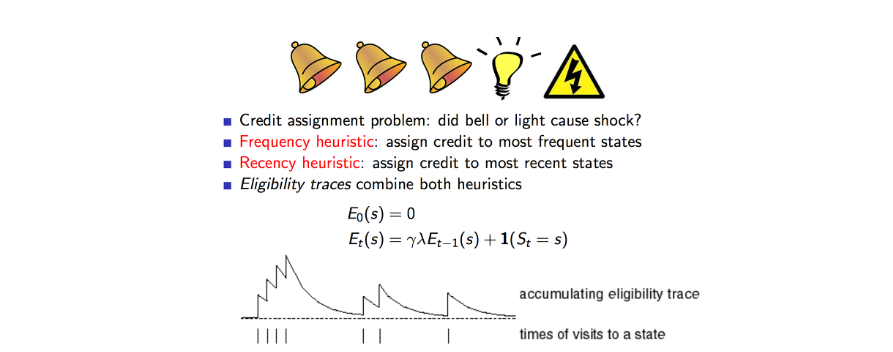
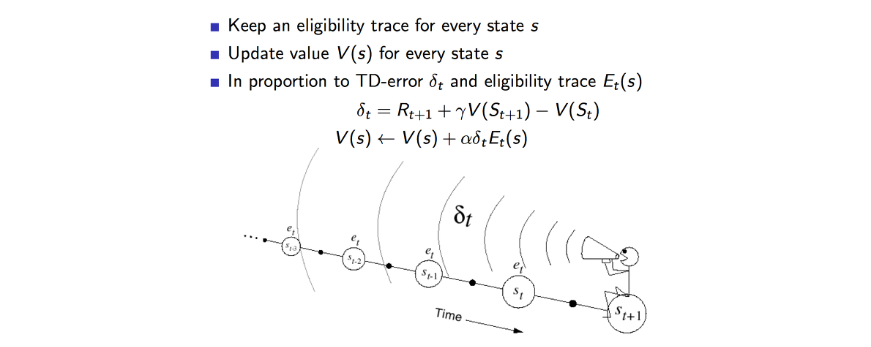
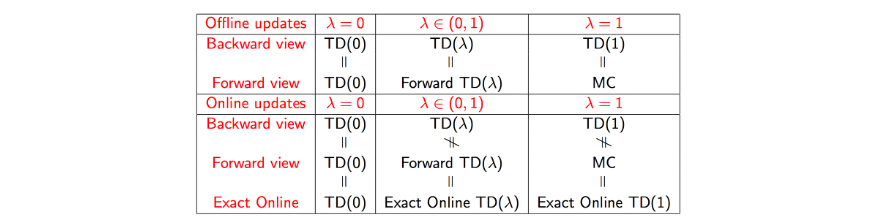
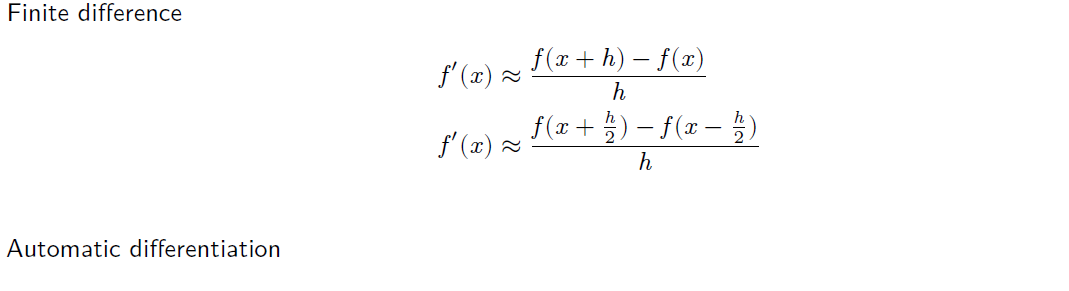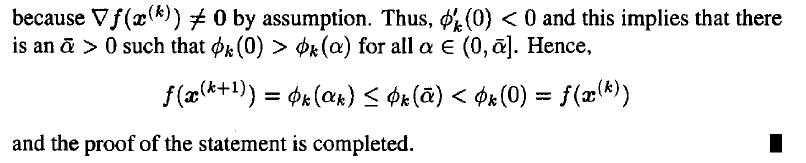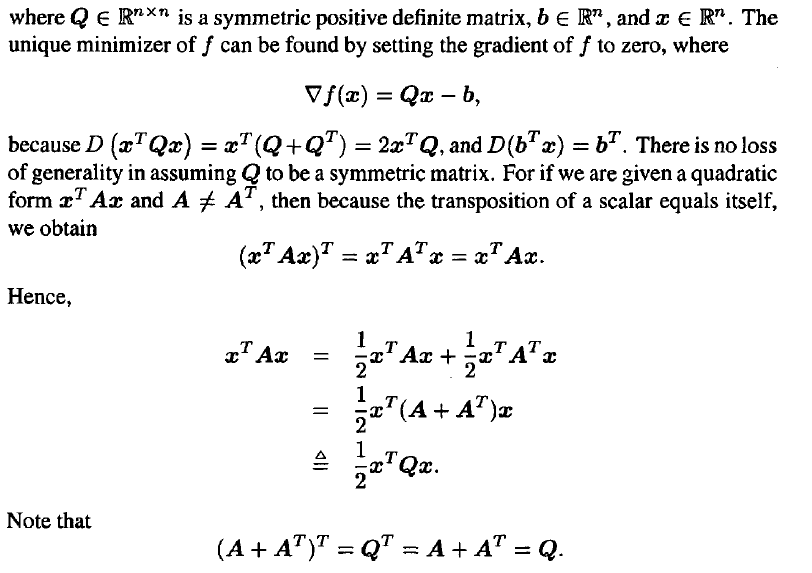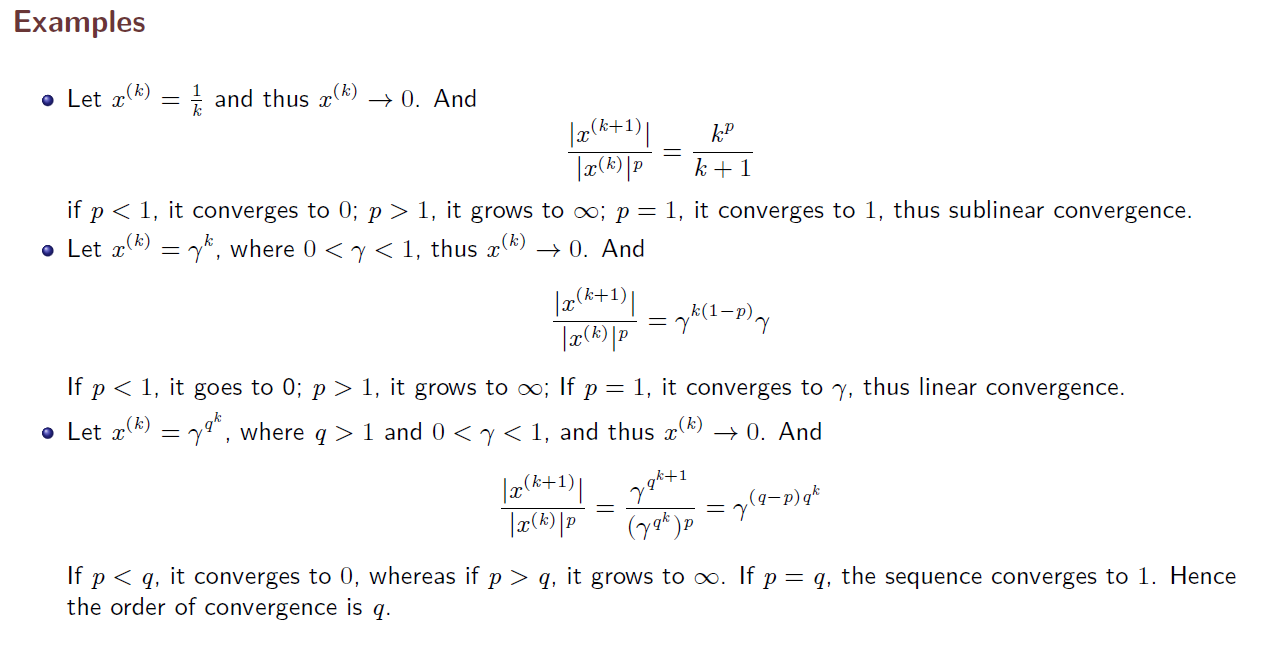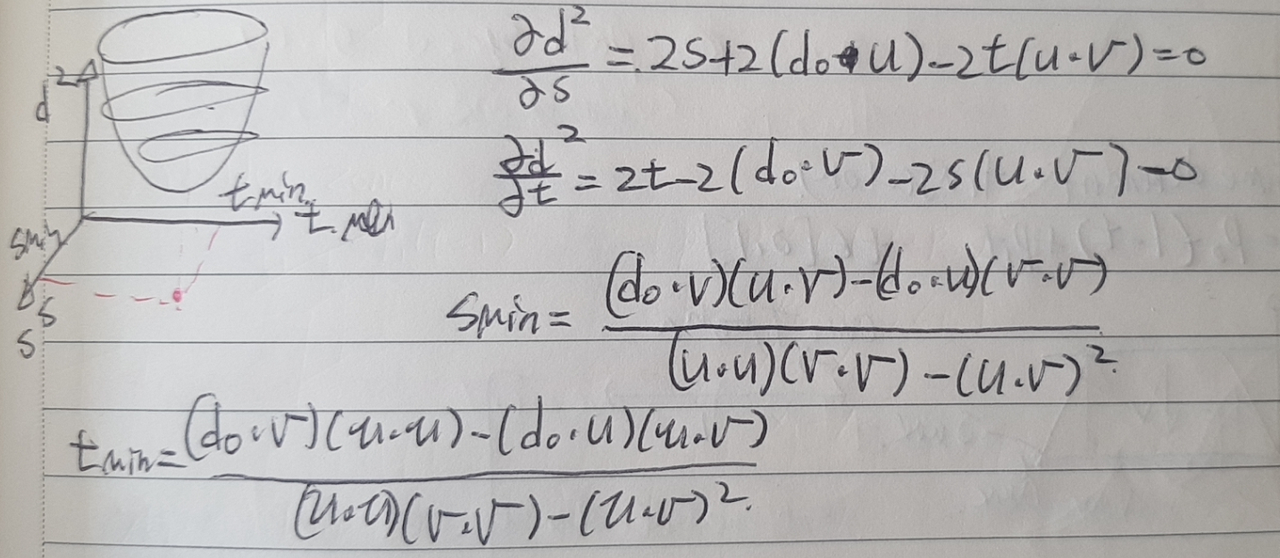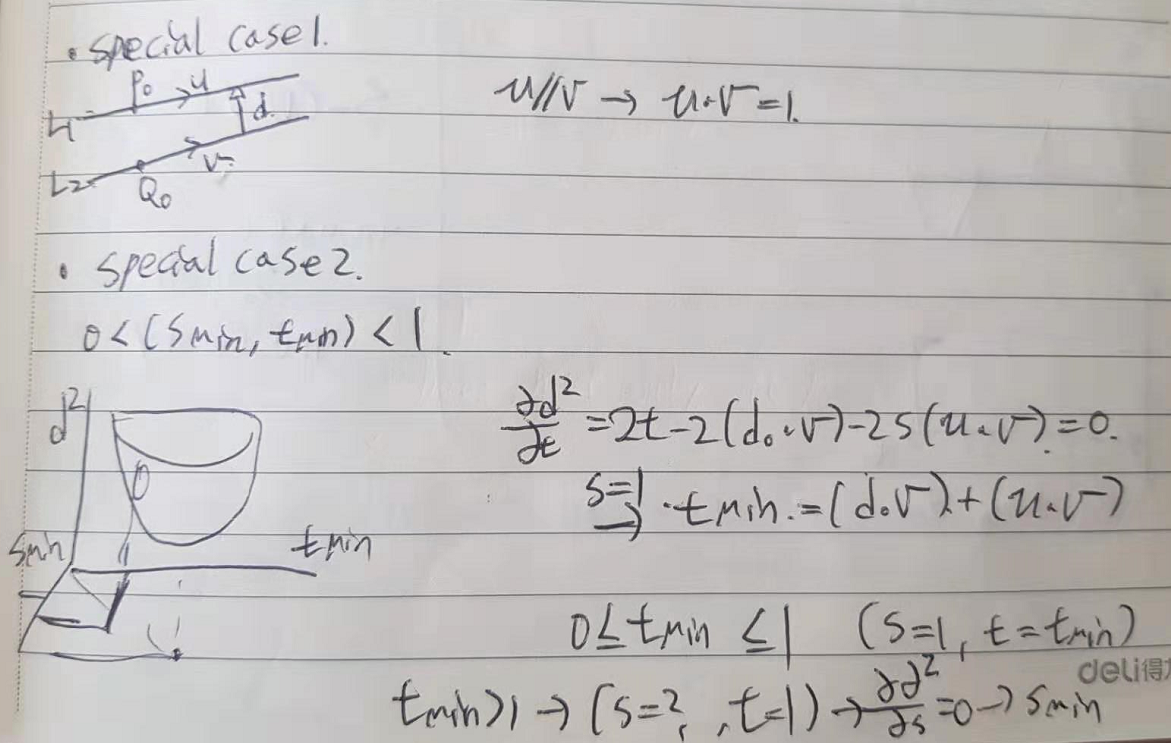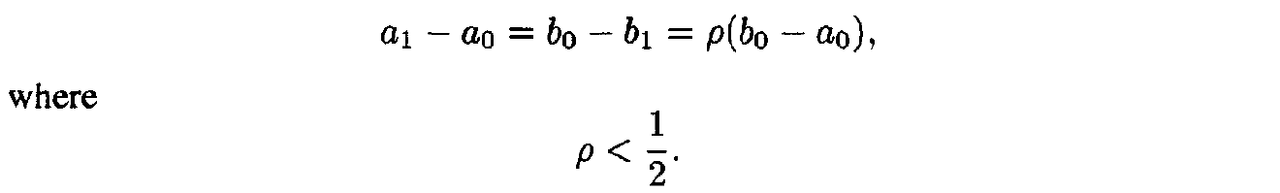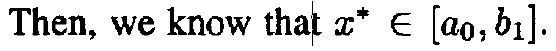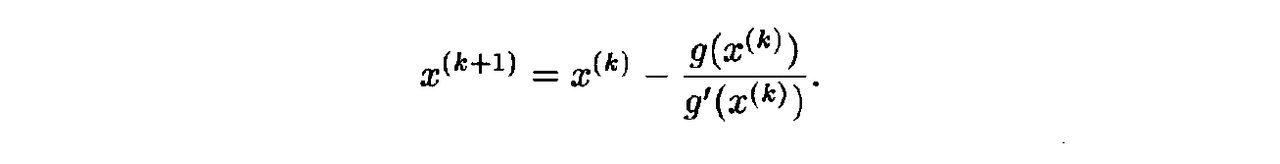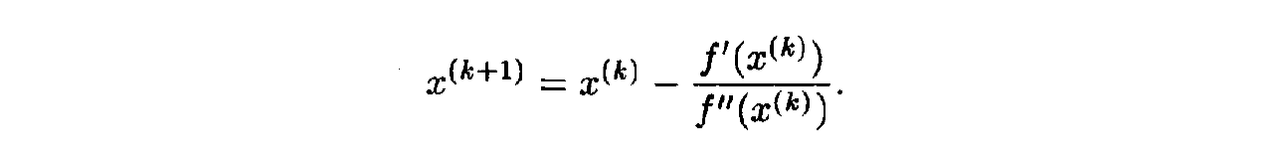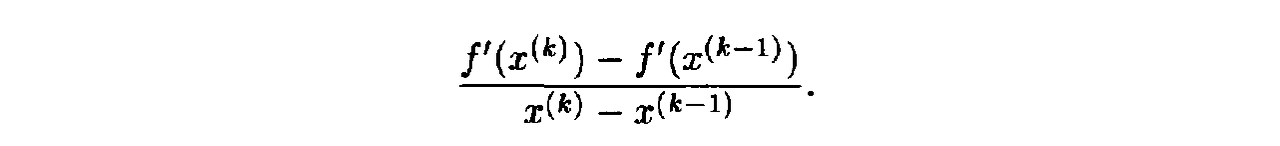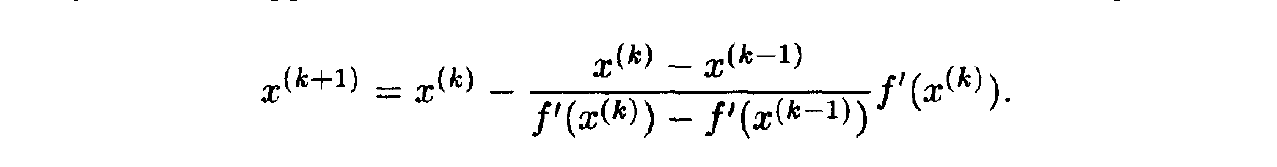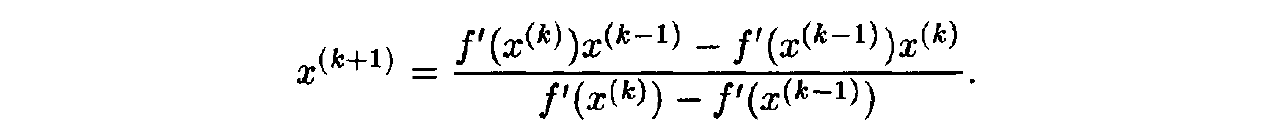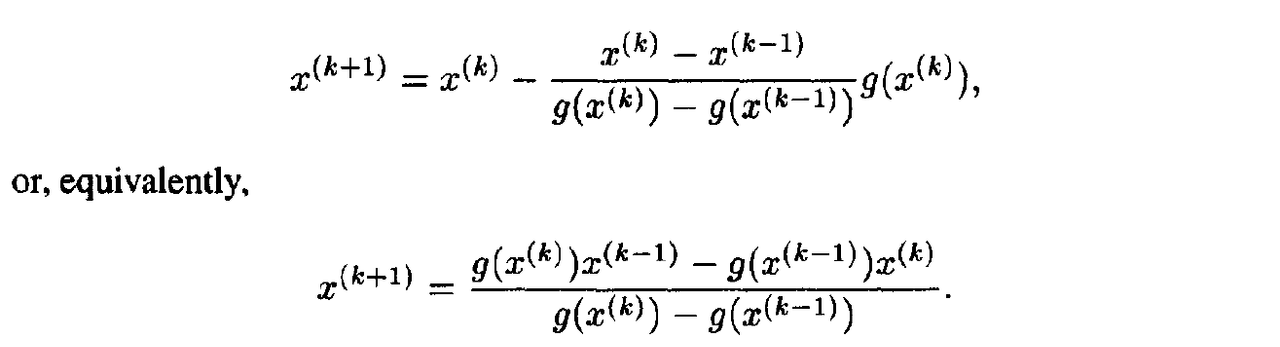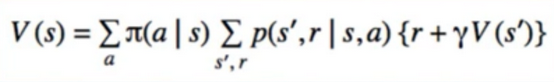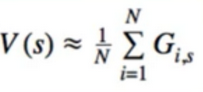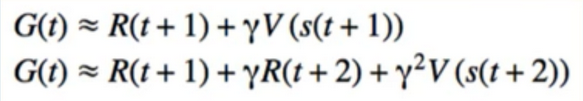8. Gradient Methods
08 Oct 2019 | Optimization method
1. Gradient Methods Introduction
- we consider a class of search methods for real-valued functions on $R^n$
- we use terms like level sets, normal vectors, tangent vectors, and so on
- Recall that a level set of a function f:$R^n$ -> R is the set of points x satisfying f(x) = c for some constant c.
- simple and intuitive
- every iteration is inexpensive
- does not require second derivatives
- extensions: nonsmooth optimization, combining with duality splitting, coordinate descent, alternating direction, stochastic, online learning
- suitable for large-scale problem, parallelization
2. Geometric interpretation of gradients and gradient descent
- ∇f($x_0$),if it is not zero, is orthogonal to the tangent of the level set curves of f passing $x_0$ on the level set f(x) = c, point outward(点向外)
- Thus, the direction of maximum rate of increase of a real-valued differentiable function at a point is orthogonal to the level set of the function through that point.
- In other words, the gradient acts in such a direction that for a given small displacement, the function f increases more in the direction of the gradient than in any other direction
- To prove this statement, recall that <∇f(x),d>, IIdII = 1, is the rate of increase of f in the direction d at the point x By the Cauchy-Schwarz inequality,
- Thus, the direction in which ∇f(x) points the direction of maximum rate of increase of f at x.
- The direction in which —∇f(x) points is the direction of maximum rate of decrease of f at x.
- Hence, the direction of negative gradient is a good direction to search if we want to find a function minimizer
- We refer to the above as a gradient descent algorithm (or simply a gradient algorithm).
- The gradient varies as the search proceeds, tending to zero as we approach the minimizer.
- We have the option of either taking very small steps and re-evaluating the gradient at every step, or we can take large steps each time.
- The first approach results in a laborious method of reaching the minimizer, whereas the second approach may result in a more zigzag path to the minimizer.
- The advantage of the second approach is a possibly fewer number of the gradient evaluations.
- Among many different methods that use the above philosophy(思想体系) the most popular is the method of steepest descent
- Gradient methods are simple to implement and often perform well.
3. Descent direction
4. Classical Gradient Method
- Small stepsizes: iterations are more likely converge, but it might requires more iteration and thus evaluations of ∇f
- Large step sizes: better use of ∇f(x) and it may reduce the total number of iterations, but it can cause oversmoothing and zig-zags which lead to divergent iterations
- Choice of stepsizes: fixed:
k constant; 1D line search (backtracking, exact, Barzilai-Borwein with nonmonotone line search)
5. Stopping Criteria
6. Calculation of Gradients
- Analytic form: use pen and paper or Mathematica/Matlab
7. The method of steepest descent
- Also known as gradient descent with exact line search
- The method of steepest descent is a gradient algorithm where the step size $α_k$ is chosen to achieve the maximum amount of decrease of the objective function at each individual step.
- Stepsize $α_k$ is determined by
- For quadratic program, $α_k$ has closed form.
- For problem with inexpensive evaluation values but expensive gradient evaluations
- To summarize, the steepest descent algorithm proceeds as follows: at each step, starting from the point $x^k$, we conduct a line search in the direction -∇f($x^k$) until a minimizer, x^(k+1),is found.
8. orthogonality
9. Function Decreasing
- relative(比较的)
10. Steepest descent for quadratic programming
11. Convergence for quadratic programming
- The method of steepest descent is an example of an iterative algorithm.
- This means that the algorithm generates a sequence of points, each calculated on the basis of the points preceding it.
- The method is a descent method because as each new point is generated by the algorithm, the corresponding value of the objective function decreases in value (i.e., the algorithm possesses the descent property).
- We say that an iterative algorithm is globally convergent if for any arbitrary starting point the algorithm is guaranteed to generate a sequence of points converging to a point that satisfies the FONC for a minimizer.
- When the algorithm is not globally convergent, it may still generate a sequence that converges to a point satisfying the FONC, provided the initial point is sufficiently close to the point.
- In this case, we say that the algorithm is locally convergent.
- How close to a solution point we need to start for the algorithm to converge depends on the local convergence properties of the algorithm.
- related issue of interest pertaining to a given locally or globally convergent algorithm is the rate of convergence; that is, how fast the algorithm converges to a solution point.
- Monotonically (无变化地)
Optimization method - Standford University
https://www.youtube.com/results?search_query=convex+function
1. Gradient Methods Introduction
- we consider a class of search methods for real-valued functions on $R^n$
- we use terms like level sets, normal vectors, tangent vectors, and so on
- Recall that a level set of a function f:$R^n$ -> R is the set of points x satisfying f(x) = c for some constant c.
- simple and intuitive
- every iteration is inexpensive
- does not require second derivatives
- extensions: nonsmooth optimization, combining with duality splitting, coordinate descent, alternating direction, stochastic, online learning
- suitable for large-scale problem, parallelization
2. Geometric interpretation of gradients and gradient descent
- ∇f($x_0$),if it is not zero, is orthogonal to the tangent of the level set curves of f passing $x_0$ on the level set f(x) = c, point outward(点向外)
- Thus, the direction of maximum rate of increase of a real-valued differentiable function at a point is orthogonal to the level set of the function through that point.
- In other words, the gradient acts in such a direction that for a given small displacement, the function f increases more in the direction of the gradient than in any other direction
- To prove this statement, recall that <∇f(x),d>, IIdII = 1, is the rate of increase of f in the direction d at the point x By the Cauchy-Schwarz inequality,
- Thus, the direction in which ∇f(x) points the direction of maximum rate of increase of f at x.
- The direction in which —∇f(x) points is the direction of maximum rate of decrease of f at x.
- Hence, the direction of negative gradient is a good direction to search if we want to find a function minimizer
- We refer to the above as a gradient descent algorithm (or simply a gradient algorithm).
- The gradient varies as the search proceeds, tending to zero as we approach the minimizer.
- We have the option of either taking very small steps and re-evaluating the gradient at every step, or we can take large steps each time.
- The first approach results in a laborious method of reaching the minimizer, whereas the second approach may result in a more zigzag path to the minimizer.
- The advantage of the second approach is a possibly fewer number of the gradient evaluations.
- Among many different methods that use the above philosophy(思想体系) the most popular is the method of steepest descent
- Gradient methods are simple to implement and often perform well.
3. Descent direction
4. Classical Gradient Method
- Small stepsizes: iterations are more likely converge, but it might requires more iteration and thus evaluations of ∇f
- Large step sizes: better use of ∇f(x) and it may reduce the total number of iterations, but it can cause oversmoothing and zig-zags which lead to divergent iterations
- Choice of stepsizes: fixed: k constant; 1D line search (backtracking, exact, Barzilai-Borwein with nonmonotone line search)
5. Stopping Criteria
6. Calculation of Gradients
- Analytic form: use pen and paper or Mathematica/Matlab
7. The method of steepest descent
- Also known as gradient descent with exact line search
- The method of steepest descent is a gradient algorithm where the step size $α_k$ is chosen to achieve the maximum amount of decrease of the objective function at each individual step.
- Stepsize $α_k$ is determined by
- For quadratic program, $α_k$ has closed form.
- For problem with inexpensive evaluation values but expensive gradient evaluations
- To summarize, the steepest descent algorithm proceeds as follows: at each step, starting from the point $x^k$, we conduct a line search in the direction -∇f($x^k$) until a minimizer, x^(k+1),is found.
8. orthogonality
9. Function Decreasing
- relative(比较的)
10. Steepest descent for quadratic programming
11. Convergence for quadratic programming
- The method of steepest descent is an example of an iterative algorithm.
- This means that the algorithm generates a sequence of points, each calculated on the basis of the points preceding it.
- The method is a descent method because as each new point is generated by the algorithm, the corresponding value of the objective function decreases in value (i.e., the algorithm possesses the descent property).
- We say that an iterative algorithm is globally convergent if for any arbitrary starting point the algorithm is guaranteed to generate a sequence of points converging to a point that satisfies the FONC for a minimizer.
- When the algorithm is not globally convergent, it may still generate a sequence that converges to a point satisfying the FONC, provided the initial point is sufficiently close to the point.
- In this case, we say that the algorithm is locally convergent.
- How close to a solution point we need to start for the algorithm to converge depends on the local convergence properties of the algorithm.
- related issue of interest pertaining to a given locally or globally convergent algorithm is the rate of convergence; that is, how fast the algorithm converges to a solution point.
- Monotonically (无变化地) Optimization method - Standford University
https://www.youtube.com/results?search_query=convex+function